Artificial
Intelligence 3E
foundations of computational agents
17.4 Existence and Identity Uncertainty
The models of Section 17.3 are concerned with relational uncertainty; uncertainty about whether a relation is true of some entities. For example, a probabilistic model of for , whether different people like each other, could depend on properties of and and other relations they are involved in. A probabilistic model for is about whether people like themselves. Models about who likes whom may be useful, for example, for a tutoring agent to determine whether two people should work together.
The problem of identity uncertainty concerns uncertainty of whether two symbols (terms or descriptions) are equal (denote the same entity).
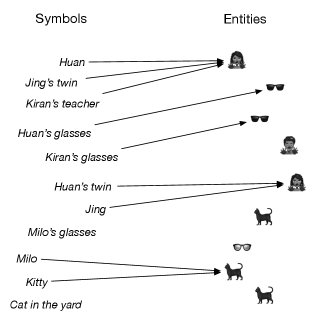
Example 17.12.
Figure 17.13 shows the denotation for some symbols; each arrow indicates what entity a symbol denotes. HuanJing’s twin, because they denote the same entity. Huan’s glassesKiran’s glasses, because they denote different pairs of glasses, even though the glasses might be identical; they would only be equal if they shared the same pair of glasses. Milo’s glasses might not exist because Milo doesn’t have a pair of glasses.
Identity partitions the symbols. Huan, Jing’s twin, and Kiran’s teacher are in the same partition as they denote the same entity. They are in a different partition from Jing. The symbols with no entity, Milo’s glasses and cat in the yard, can be in a special partition.
Identity uncertainty is a problem for medical systems, where it is important to determine whether the person who is interacting with the system now is the same person as one who visited yesterday. This problem is particularly difficult if the patient is non-communicative or wants to deceive the system, for example, to get drugs. This problem is also referred to as record linkage, as the problem is to determine which (medical) records are for the same person. This problem also arises in citation matching, determining if authors on different papers are the same person, or if two citations denote the same paper.
Identity uncertainty is computationally intractable because it is equivalent to partitioning the symbols. For citation matching, the partition is over the citations; the citations denoting the same paper are in the same partition. The number of partitions of items is called the Bell number, which grows faster than any exponential in . The most common way to find the distribution over partitions is to use Markov-chain Monte Carlo (MCMC). Given a partition, entities can be moved to different partitions or to new partitions.
The techniques of the previous sections assumed the entities are known to exist. Given a description, the problem of determining whether there exists an entity that fits the description is the problem of existence uncertainty. Existence uncertainty is problematic because there may be no entities who fit a description or there may be multiple entities. For example, for the description “the cat in the yard”, there may be no cats in the yard or there might be multiple cats. You cannot give properties to non-existent entities, because entities that do not exist do not have properties. If you want to give a name to an entity that exists, we need to be concerned about which entity you are referring to if there are multiple entities that exist.
One particular case of existence uncertainty is number uncertainty, about the number of entities that exist. For example, a purchasing agent may be uncertain about the number of people who would be interested in a package tour, and whether to offer the tour depends on the number of people who may be interested.
Reasoning about existence uncertainty can be tricky if there are complex roles involved, and the problem is to determine whether there are entities to fill the roles. Consider a purchasing agent who must find an apartment for Sam and Sam’s child Chris. Whether Sam wants an apartment probabilistically depends, in part, on the size of Sam’s room and the color of Chris’s room. However, entity apartments do not come labeled with Sam’s room and Chris’s room, and there may not exist a room for each of them. Given a model of an apartment Sam would want, it is not obvious how to condition on the observations.



