14 Multiagent Systems 14.1 Multiagent Framework 14.3 Solving Perfect Information Games

14.2 Representations of Games

A mechanism represents the actions available to each agent and the (distribution over) outcomes for their joint actions. There are many representations for mechanisms in games, and multiagent interactions in general, that have been proposed in economics and AI. In AI, these representations typically allow the designer to model aspects of games that can be exploited for computational gain.

Three representations are presented; two of these are classic representations from economics. The first abstracts away all structure of the policies of the agents. The second models the sequential structure of games and is the foundation for much work on representing board games. The third representation moves away from the state-based representation to allow the representation of games in terms of features.

14.2.1 Normal-Form Games

The most basic representation of games is the normal-form game, also known as the strategic-form game. A normal-form game consists of

•

a finite set $I$ of agents, typically identified with the integers $I=\{1,\dots,n\}$
•

a set of actions $A_{i}$ for each agent $i\in I$
•

a utility function $u_{i}$ for each agent $i\in I$ that, given an assignment of action to every agent, returns the expected utility for agent $i$ ; each agent is trying to maximize its own utility.

An action profile is a tuple $\left<a_{1},\dots,a_{n}\right>$ , which specifies that agent $i\in I$ carries out action $a_{i}$ , where $a_{i}\in A_{i}$ . An action profile produced an outcome. Each agent has a utility over each outcome. The utility for an agent is meant to encompass everything that the agent is interested in, including fairness, altruism, and societal well-being.

Example 14.1.

The game rock–paper–scissors is a common game played by children, and there is even a world championship. Suppose there are two agents (players), Alice and Bob. There are three actions for each agent, so that

A_{Alice}=A_{Bob}=\{rock,paper,scissors\}.

For each combination of an action for Alice and an action for Bob, there is a utility for Alice and a utility for Bob.

		Bob
		$r o c k$	$p a p e r$	$s c i s s o r s$
	$r o c k$	$0,0$	$-1,1$	$1,-1$
Alice	$p a p e r$	$1,-1$	$0,0$	$-1,1$
	$s c i s s o r s$	$-1,1$	$1,-1$	0,0

Figure 14.1: Normal form for the rock–paper–scissors game

This is often drawn in a table as in Figure 14.1. This is called a payoff matrix. Alice chooses a row and Bob chooses a column, simultaneously. This gives a pair of numbers: the first number is the payoff to the row player (Alice) and the second gives the payoff to the column player (Bob). Note that the utility for each of them depends on what both players do. An example of an action profile is $\left<scissors_{Alice},rock_{Bob}\right>$ , where Alice chooses scissors and Bob chooses rock. In this action profile, Alice receives the utility of $-1$ and Bob receives the utility of $1$ . This game is a zero-sum game because one person wins only when the other loses.

This representation of a game may seem very restricted, because it only gives a one-off payoff for each agent based on single actions, chosen simultaneously, for each agent. However, the interpretation of an action in the definition is very general.

Typically, an “action” is not just a simple choice, but a strategy: a specification of what the agent will do under the various contingencies. The normal form, essentially, is a specification of the utilities given the possible strategies of the agents. This is why it is called the strategic form of a game.

More generally, the “action” in the definition of a normal-form game can be a controller for the agent. Thus, each agent chooses a controller and the utility gives the expected outcome of the controllers run for each agent in an environment. Although the examples that follow are for simple actions, the general case has an enormous number of possible actions (possible controllers) for each agent.

14.2.2 Extensive Form of a Game

Whereas the normal form of a game represents controllers as single units, it is often more natural to specify the unfolding of a game through time. The extensive form of a game is an extension of a single-agent decision tree. Let’s first give a definition that assumes the game is fully observable (called perfect information in game theory).

A perfect-information game in extensive form, or a game tree, is a finite tree where the nodes are states and the arcs correspond to actions by the agents. In particular:

•

Each internal node is labeled with an agent (or with nature). The agent is said to control the node.
•

Each arc out of a node labeled with agent $i$ corresponds to an action for agent $i$ .
•

Each internal node labeled with nature has a probability distribution over its children.
•

The leaves represent final outcomes and are labeled with a utility for each agent.

The extensive form of a game specifies a particular unfolding of the game. Each path to a leaf, called a run, specifies one particular way that the game could proceed, depending on the choices of the agents and nature.

A strategy for agent $i$ is a function from nodes controlled by agent $i$ into actions. That is, a strategy selects a child for each node that agent $i$ controls. A strategy profile consists of a strategy for each agent.

Example 14.2.

Consider a sharing game where there are two agents, Andy and Barb, and there are two identical items to be divided between them. Andy first selects how they will be divided: Andy keeps both items, they share and each person gets one item, or he gives both items to Barb. Then Barb gets to either reject the allocation and they both get nothing, or accept the allocation and they both get the allocated amount.

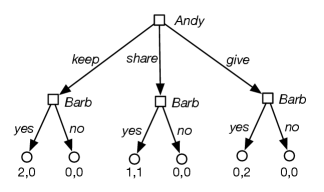
Refer to caption — Figure 14.2: Extensive form of the sharing game

The extensive form of the sharing game is shown in Figure 14.2. Andy has 3 strategies. Barb has $2^{3}=8$ strategies; one for each combination of assignments to the nodes she controls. As a result, there are 24 strategy profiles.

Given a strategy profile, each node has a utility for each agent. The utility for an agent at a node is defined recursively from the bottom up:

•

The utility for each agent at a leaf is given as part of the leaf.
•

The utility for an agent at a node controlled by that agent is the utility for the agent of the child node that is selected by the agent’s strategy.
•

The utility for agent $j$ at a node controlled by another agent $i$ is the utility for agent $j$ of the child node that is selected by agent $i$ ’s strategy.
•

The utility for agent $i$ for a node controlled by nature is the expected value of the utility for agent $i$ of the children. That is, $u_{i}(n)=\sum_{c}P(c)u_{i}(c)$ , where the sum is over the children $c$ of node $n$ , and $P(c)$ is the probability that nature will choose child $c$ .

Example 14.3.

In the sharing game, consider the following strategy profile: Andy, not knowing what Barb will do, chooses $k e e p$ . Barb chooses $n o$ , $y e s$ , $y e s$ for each of the nodes she gets to choose for. Under this strategy profile, the utility for Andy at the leftmost internal node is $0$ , the utility for Andy at the center internal node is $1$ , and the utility for Andy at the rightmost internal node is $0$ . For this strategy profile, the utility for Andy at the root is $0$ .

The preceding definition of the extensive form of a game assumes that the agents can observe the state of the world (i.e., at each stage they know which node they are at). This means that the state of the game must be fully observable. In a partially observable game or an imperfect-information game, the agents do not necessarily know the state of the world when they have to decide what to do. This includes simultaneous-action games, where more than one agent needs to decide what to do at the same time. In such cases, the agents do not know which node they are at in the game tree. To model these games, the extensive form of a game is extended to include information sets. An information set is a set of nodes, all controlled by the same agent and all with the same set of available actions. The idea is that the agent cannot distinguish the elements of the information set. The agent only knows the game state is at one of the nodes in the information set, not which of those nodes. In a strategy, the agent chooses one action for each information set; the same action is carried out at each node in the information set. Thus, in the extensive form, a strategy specifies a function from information sets to actions.

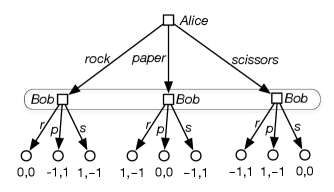
Example 14.4.

Figure 14.3 gives the extensive form for the rock–paper–scissors game of Example 14.1. The elements of the information set are in a rounded rectangle. In a strategy, Bob must treat each node in the information set the same. When Bob gets to choose his action, he does not know which action Alice has chosen.

14.2.3 Multiagent Decision Networks

The extensive form of a game is a state-based representation of the game. It is often more concise to describe states in terms of features. A multiagent decision network is a factored representation of a multiagent decision problem. It is like a decision network, except that each decision node is labeled with an agent that gets to choose a value for the node. There is a utility node for each agent specifying the utility for that agent. The parents of a decision node specify the information that will be available to the agent when it has to act.

Example 14.5.

Figure 14.4 gives a multiagent decision network for a fire alarm example.

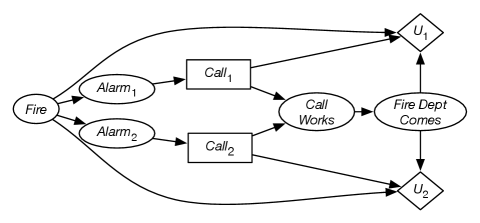
In this scenario, there are two agents, Agent 1 and Agent 2. Each has its own noisy sensor of whether there is a fire. However, if they both call, it is possible that their calls will interfere with each other and neither call will work. Agent 1 gets to choose a value for decision variable $Call_{1}$ and only observes the value for the variable $Alarm_{1}$ . Agent 2 gets to choose a value for decision variable $Call_{2}$ and only observes the value for the variable $Alarm_{2}$ . Whether the call works depends on the values of $Call_{1}$ and $Call_{2}$ . Whether the fire department comes depends on whether the call works. Agent 1’s utility depends on whether there was a fire, whether the fire department comes, and whether they called – similarly for Agent 2.

A multiagent decision network can be converted into a normal-form game; however, the number of strategies may be enormous. If a decision variable has $d$ states and $n$ binary parents, there are $2^{n}$ assignments of values to parents and so $d^{2^{n}}$ strategies. That is just for a single decision node; more complicated networks are even bigger when converted to normal form. Thus, algorithms that depend on enumerating strategies are impractical for anything but the smallest multiagent decision networks.

Other representations exploit other structures in multiagent settings. For example, the utility of an agent may depend on the number of other agents who do some action, but not on their identities. An agent’s utility may depend on what a few other agents do, not directly on the actions of all other agents. An agent’s utility may only depend on what the agents at neighboring locations do, and not on the identity of these agents or on what other agents do.

Artificial Intelligence 3E