Artificial
Intelligence 3E
foundations of computational agents
11.4 Instrumental Variables
Sometimes it is difficult to manipulate a variable; for example, someone carrying out a medical trial can’t force someone to take a drug, all they can do is try to convince them, for example by paying them. An instrumental variable is a variable that can be used as a surrogate for a variable that is difficult to manipulate. Observable or controllable variable is an instrumental variable for variable in predicting if:
-
•
is independent of the possible confounders between and . One way to ensure independence is to randomize .
-
•
is independent of given . The only way for to affect is to affect .
-
•
There is a strong association between and .
The variable can be used to manipulate , thus giving an artificial experiment. There is no causation between and that holds for all conditional probabilities in this setup, so the do-calculus cannot be used to infer causation. However, based on the actual probabilities, some bounds can be inferred, as in the following example.
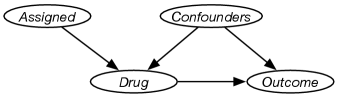
Example 11.11.
Suppose you wanted to know the effect of a drug on a disease, that is, you want to compute , how likely is the disease if someone takes the drug versus not taking the drug. You create a randomized experiment where some people are assigned the drug and some are assigned a placebo. However, some people might not take the pill prescribed for them.
Figure 11.10 shows a model of the relationship between being assigned a drug and taking a drug, and the effect on a disease. You don’t know what the possible confounders are, and so can’t measure them. The participants were assigned the drug randomly and so that is independent of the confounders. The participants did not know whether they were assigned the drug or a placebo, so it is reasonable to assume that assignment is also independent of the outcome given the drug.
The do-calculus does not help here; the propensity to not take the drug might be highly correlated with the outcome. The people who would not take the drug might be those who would have a good (or bad) outcome. There is no method that can produce an answer based only on the graphical model.
Consider the following fictional data:
| Assigned | Drug | Outcome | Count |
|---|---|---|---|
| true | true | good | 300 |
| true | true | bad | 50 |
| true | false | good | 25 |
| true | false | bad | 125 |
| false | true | good | 0 |
| false | true | bad | 0 |
| false | false | good | 100 |
| false | false | bad | 400 |
No one who was not assigned the drug, actually took it, which is reasonable for a clinical trial for a new drug.
While you may not be able to determine , it is possible to bound the effect by considering what would have happened to the non-compliers (those assigned the drug who did not take it). The following analysis ignores regularization, and so is expected to overfit.
At one extreme, none of the non-compliers would have had a good outcome if they had been forced to take the drug. In this case, 300 of the patients would have a good outcome. Thus, intervening on the drug would have resulted in 300/500 having a good outcome.
At the other extreme, all of the non-compliers would have had a good outcome if they had been forced to take the drug. In this case, 450 of the patients would have a good outcome. Thus, intervening on the drug would result in 450/500 having a good outcome.
Putting the two extremes together gives
Because there was full compliance of those not assigned the drug:
In this analysis, the outcome of those that were assigned the drug and didn’t take it was ignored, but the non-compliance cannot be ignored. Just removing non-compliant people from the sample, resulting in the conclusion that the outcome was good with probability 3/4 when the drug was taken, would be equivalent to assuming there are no confounders, which may not be a reasonable assumption.
It is often useful to consider the effect of the drug as the difference between (or ratio of) the outcome when the drug was taken and the outcome when the drug was not taken.
It is also possible to make other assumptions to allow for inference from instrumental variables. A common assumption for real-valued variables is that each variable is a linear function of its parents. Solving for the coefficients can give a unique solution.



