Third edition of Artificial Intelligence: foundations of computational agents, Cambridge University Press, 2023 is now available (including the full text).
12.4.2 Definite Resolution with Variables
The propositional top-down proof procedure can be extended to the case with variables by allowing instances of rules to be used in the derivation.
A generalized answer clause is of the form
where t1,...,tk are terms and a1,...,am are atoms. The use of yes enables answer extraction: determining which instances of the query variables are a logical consequence of the knowledge base.
Initially, the generalized answer clause for query q is
yes(V1,...,Vk)←q,
where V1,...,Vk are the variables that appear in q. Intuitively this means that an instance of yes(V1,...,Vk) is true if the corresponding instance of the query is true.
The proof procedure maintains a current generalized answer clause.
At each stage, the algorithm selects an atom ai in the body of the generalized answer clause. It then chooses a clause in the knowledge base whose head unifies with ai. The SLD resolution of the generalized answer clause yes(t1,...,tk)←a1∧a2∧...∧am on ai with the chosen clause
where ai and a have most general unifier σ, is the answer clause
where the body of the chosen clause has replaced ai in the answer clause, and the MGU is applied to the whole answer clause.
An SLD derivation is a sequence of generalized answer clauses γ0, γ1, ..., γn such that
- γ0 is the answer clause
corresponding to the original query. If the query is
q, with free variables
V1,...,Vk, the initial generalized answer
clause γ0 is
yes(V1,...,Vk)←q.
- γi is obtained by selecting an atom ai in the body of
γi-1; choosing a copy of a clause a←b1∧...∧bp in the knowledge
base whose head, a, unifies with ai; replacing ai with the
body, b1∧...∧bp; and applying the unifier to the
whole resulting answer clause.
The main difference between this and the propositional top-down proof procedure is that, for clauses with variables, the proof procedure must take copies of clauses from the knowledge base. The copying renames the variables in the clause with new names. This is both to remove name clashes between variables and because a single proof may use different instances of a clause.
- γn is an answer. That is,
it is of the form
yes(t1,...,tk)←.
When this occurs, the algorithm returns the answer
V1=t1,...,Vk=tk.
Notice how the answer is extracted; the arguments to yes keep track of the instances of the variables in the initial query that lead to a successful proof.
2: Inputs
3: KB: a set definite clauses
4: Query q: a set of atoms to prove, with variables V1,...,Vk
5: Output
6: substitution θ if KB
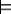 q θ and fail
otherwise
q θ and fail
otherwise
7: Local
8: G is a generalized answer clause
9: Set G to generalized answer clause yes(V1,...,Vk)←q
10: while (G is not an answer)
11: Suppose G is yes(t1,...,tk)←a1∧a2∧...∧am
12: select atom ai in the body of G
13: choose clause a←b1∧...∧bp in KB
14: Rename all variables in a←b1∧...∧bp to have new names
15: Let σ be unify(ai,a). Fail if unify returns ⊥.
16: assign G the answer clause: (yes(t1,...,tk)←a1∧...∧ai-1 ∧b1∧...∧bp∧ai+1∧...∧am)σ
17:
18: return V1=t1,...,Vk=tk where G is yes(t1,...,tk)←
A non-deterministic procedure that answers queries by finding SLD derivations is given in Figure 12.3. This is non-deterministic in the sense that all derivations can be found by making appropriate choices that do not fail. If all choices fail, the algorithm fails, and there are no derivations. The choose is implemented using search. This algorithm assumes that unify(ai,a) returns an MGU of ai and a, if there is one, and ⊥ if they do not unify. Unification is defined in the next section.
ask two_doors_east(R,r107).
Figure
12.4 shows a successful derivation with answer R=r111.resolve with two_doors_east(E1,W1) ←
imm_east(E1,M1) ∧imm_east(M1,W1).
substitution: {E1/R,W1/r107}
yes(R)←imm_east(R,M1) ∧imm_east(M1,r107)
select leftmost conjunct
resolve with imm_east(E2,W2)←imm_west(W2,E2)
substitution: {E2/R,W2/M1}
yes(R)←imm_west(M1,R) ∧imm_east(M1,r107)
select leftmost conjunct
resolve with imm_west(r109,r111)
substitution: {M1/r109,R/r111}
yes(r111)←imm_east(r109,r107)
resolve with imm_east(E3,W3)←imm_west(W3,E3)
substitution: {E3/r109,W3/r107}
yes(r111)←imm_west(r107,r109)
resolve with imm_west(r107,r109)
substitution: {}
yes(r111)←
Note that this derivation used two instances of the rule
imm_east(E,W) ←imm_west(W,E).
One instance eventually substituted r111 for E, and one instance substituted r109 for E.
Some choices of which clauses to resolve against may have resulted in a partial derivation that could not be completed.



