Third edition of Artificial Intelligence: foundations of computational agents, Cambridge University Press, 2023 is now available (including the full text).
12.4.1 Bottom-up Procedure with Variables
The propositional bottom-up proof procedure can be extended to Datalog by using ground instances of the clauses. A ground instance of a clause is obtained by uniformly substituting constants for the variables in the clause. The constants required are those appearing in the knowledge base or in the query. If there are no constants in the knowledge base or the query, one must be invented.
q(b).
r(a).
s(W) ←r(W).
p(X,Y) ←q(X) ∧s(Y).
The set of all ground instances is
q(b).
r(a).
s(a) ←r(a).
s(b) ←r(b).
p(a,a) ←q(a) ∧s(a).
p(a,b) ←q(a) ∧s(b).
p(b,a) ←q(b) ∧s(a).
p(b,b) ←q(b) ∧s(b).
The propositional bottom-up proof procedure of Section 5.2.2.1 can be applied to the grounding to derive q(a), q(b), r(a), s(a), p(a,a), and p(b,a) as the ground instances that are logical consequences.
g ←p(W,W).
The bottom-up proof procedure must invent a new constant symbol, say c. The set of all ground instances is then
g ←p(c,c).
The propositional bottom-up proof procedure will derive p(c,c) and g.
If the query was ask p(a,d), the set of ground instances would change to reflect these constants.
The bottom-up proof procedure applied to the grounding of the knowledge base is sound, because each instance of each rule is true in every model. This procedure is essentially the same as the variable-free case, but it uses the set of ground instances of the clauses, all of which are true by definition.
This procedure is also complete for ground atoms. That is, if a ground atom is a consequence of the knowledge base, it will eventually be derived. To prove this, as in the propositional case, we construct a particular generic model. A model must specify what the constants denote. A Herbrand interpretation is an interpretation where the the domain is symbolic and consists of all constants of the language. An individual is invented if there are no constants. In a Herbrand interpretation, each constant denotes itself.
Consider the Herbrand
interpretation where the ground instances of the relations that are
eventually derived by the bottom-up procedure with a fair selection
rule are true. It is easy to see that this Herbrand interpretation is a model of the rules
given. As in the variable-free case,
it is a minimal model in that it has the fewest true atoms of any model. If
KB 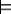 g for ground atom g, then g is true in the minimal
model and, thus, is eventually derived.
g for ground atom g, then g is true in the minimal
model and, thus, is eventually derived.
imm_east(r105,r103)
imm_east(r107,r105)
imm_east(r109,r107)
imm_east(r111,r109)
imm_east(r129,r131)
imm_east(r127,r129)
imm_east(r125,r127)
Next, the next_door relations that follow can be added to the set of consequences, including
next_door(r103,r101)
The two_door_east relations can be added to the set of consequences, including
two_door_east(r107,r103)
Finally, the west relations that follow can be added to the set of consequences.



