Third edition of Artificial Intelligence: foundations of computational agents, Cambridge University Press, 2023 is now available (including the full text).
9.5 Decision Processes
The decision networks of the previous section were for finite-stage, partially observable domains. In this section, we consider indefinite horizon and infinite horizon problems.
Often an agent must reason about an ongoing process or it does not know how many actions it will be required to do. These are called infinite horizon problems when the process may go on forever or indefinite horizon problems when the agent will eventually stop, but where it does not know when it will stop. To model these situations, we augment the Markov chain with actions. At each stage, the agent decides which action to perform; the resulting state depends on both the previous state and the action performed. For ongoing processes, you do not want to consider only the utility at the end, because the agent may never get to the end. Instead, an agent can receive a sequence of rewards. These rewards incorporate the action costs in addition to any prizes or penalties that may be awarded. Negative rewards are called punishments. Indefinite horizon problems can be modeled using a stopping state. A stopping state or absorbing state is a state in which all actions have no effect; that is, when the agent is in that state, all actions immediately return to that state with a zero reward. Goal achievement can be modeled by having a reward for entering such a stopping state.
We only consider stationary models where the state transitions and the rewards do not depend on the time.
A Markov decision process or an MDP consists of
- S, a set of states of the world.
- A, a set of actions.
- P:S×S ×A →[0,1], which specifies the
dynamics. This is written P(s'|s,a), where
∀s ∈S ∀a ∈A ∑s'∈S P(s'|s,a) = 1.
In particular, P(s'|s,a) specifies the probability of transitioning to state s' given that the agent is in state s and does action a.
- R:S×A ×S →R, where R(s,a,s') gives the expected immediate reward from doing action a and transitioning to state s' from state s.
Both the dynamics and the rewards can be stochastic; there can be some randomness in the resulting state and reward, which is modeled by having a distribution over the resulting state and by R giving the expected reward. The outcomes are stochastic when they depend on random variables that are not modeled in the MDP.
A finite part of a Markov decision process can be depicted using a decision network as in Figure 9.12.
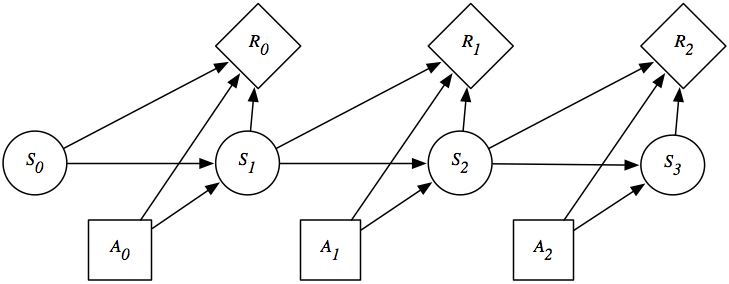
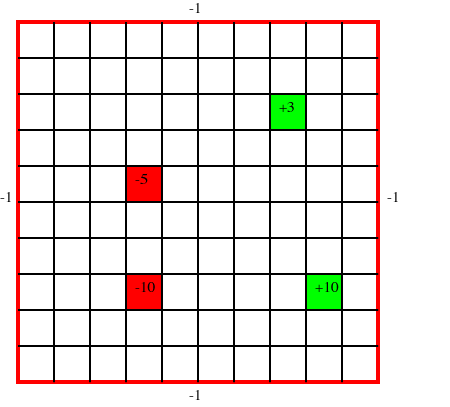
Figure 9.13 shows a 10×10 grid world, where the robot can choose one of four actions: up, down, left, or right. If the agent carries out one of these actions, it has a 0.7 chance of going one step in the desired direction and a 0.1 chance of going one step in any of the other three directions. If it bumps into the outside wall (i.e., the square computed as above is outside the grid), there is a penalty of 1 (i.e., a reward of -1) and the agent does not actually move. There are four rewarding states (apart from the walls), one worth +10 (at position (9,8); 9 across and 8 down), one worth +3 (at position (8,3)), one worth -5 (at position (4,5)), and one worth -10 (at position (4,8)). In each of these states, the agent gets the reward after it carries out an action in that state, not when it enters the state. When the agent reaches the state (9,8), no matter what it does at the next step, it is flung, at random, to one of the four corners of the grid world.
Note that, in this example, the reward is be a function of both the initial state and the final state. The way to tell if the agent bumped into the wall is if the agent did not actually move. Knowing just the initial state and the action, or just the final state and the action, does not provide enough information to infer the reward.
As with decision networks, the designer also has to consider what information is available to the agent when it decides what to do. There are two common variations:
- In a fully observable Markov decision process, the agent gets to observe the current state when deciding what to do.
- A partially observable Markov decision process (POMDP) is a combination of an MDP and a hidden Markov model. At each time point, the agent gets to make some observations that depend on the state. The agent only has access to the history of observations and previous actions when making a decision. It cannot directly observe the current state.
To decide what to do, the agent compares different sequences of rewards. The most common way to do this is to convert a sequence of rewards into a number called the value or the cumulative reward. To do this, the agent combines an immediate reward with other rewards in the future. Suppose the agent receives the sequence of rewards:
r1,r2,r3,r4,....
There are three common ways to combine rewards into a value V:
- total reward:
- V = ∑i=1∞ ri. In this case, the value is the sum of all of the rewards. This works when you can guarantee that the sum is finite; but if the sum is infinite, it does not give any opportunity to compare which sequence of rewards is preferable. For example, a sequence of $1 rewards has the same total as a sequence of $100 rewards (both are infinite). One case where the reward is finite is when there is a stopping state; when the agent always has a non-zero probability of entering a stopping state, the total reward will be finite.
- average reward:
- V = limn→∞ (r1+···+rn)/n. In this case, the agent's value is the average of its rewards, averaged over for each time period. As long as the rewards are finite, this value will also be finite. However, whenever the total reward is finite, the average reward is zero, and so the average reward will fail to allow the agent to choose among different actions that each have a zero average reward. Under this criterion, the only thing that matters is where the agent ends up. Any finite sequence of bad actions does not affect the limit. For example, receiving $1,000,000 followed by rewards of $1 has the same average reward as receiving $0 followed by rewards of $1 (they both have an average reward of $1).
- discounted reward:
-
V = r1+γr2+γ2 r3 + ···+
γi-1 ri+···, where γ, the discount factor, is a
number in the range 0 ≤ γ< 1. Under this criterion,
future rewards are worth less than the current reward. If γ was 1, this would be
the same as the total reward. When γ=0, the agent ignores
all future rewards. Having 0 ≤ γ< 1 guarantees that,
whenever the rewards are finite, the total value will also be finite.
We can rewrite the discounted reward as
V = ∑i=1∞γi-1ri = r1+γr2+γ2 r3 + ···+ γi-1 ri+··· = r1+ γ(r2 + γ(r3 + ...)). Suppose Vk is the reward accumulated from time k:
Vk =rk+γ(rk+1 + γ( rk+2 + ...)) = rk + γVk+1. To understand the properties of Vk, suppose S = 1+ γ+ γ2 + γ3 + ..., then S=1+γS. Solving for S gives S = 1/(1-γ). Thus, under the discounted reward, the value of all of the future is at most 1/(1-γ) times as much as the maximum reward and at least 1/(1-γ) times as much as the minimum reward. Therefore, the eternity of time from now only has a finite value compared with the immediate reward, unlike the average reward, in which the immediate reward is dominated by the cumulative reward for the eternity of time.
In economics, γ is related to the interest rate: getting $1 now is equivalent to getting $(1+i) in one year, where i is the interest rate. You could also see the discount rate as the probability that the agent survives; γ can be seen as the probability that the agent keeps going. The rest of this book considers a discounted reward.
A stationary policy is a function π:S→A. That is, it assigns an action to each state. Given a reward criterion, a policy has an expected value for every state. Let Vπ(s) be the expected value of following π in state s. This specifies how much value the agent expects to receive from following the policy in that state. Policy π is an optimal policy if there is no policy π' and no state s such that Vπ'(s)>Vπ(s). That is, it is a policy that has a greater or equal expected value at every state than any other policy.
For infinite horizon problems, a stationary MDP always has an optimal stationary policy. However, this is not true for finite-stage problems, where a non-stationary policy might be better than all stationary policies. For example, if the agent had to stop at time n, for the last decision in some state, the agent would act to get the largest immediate reward without considering the future actions, but for earlier decisions at the same state it may decide to get a lower reward immediately to obtain a larger reward later.



