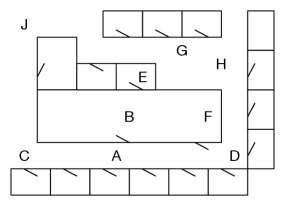
Consider the robot delivery domain of Figure 3.1, where there are offices around a central lab. The only way a robot can get through a doorway is to push the door open in the direction shown. The task is to find a path from one location to another. Assuming that the agent can use a lower-level controller to get from one location to a neighboring location, the actions for the search are traveling between neighboring locations. This can be modeled as a state-space search problem, where the states are locations. Some of the locations in Figure 3.1 are named and used as exemplars.

Consider an example problem where the robot starts at location $A$, and the goal is to get to location $G$. Thus, $G$ is the only state that satisfies the goal. A solution is a sequence of actions that moves the robot from $A$ to $G$.

Consider a video game played on a grid, where an agent can move up, down, left, or right one step as long as the move is not blocked by a wall. The agent has to collect four coins, $C_1,\mathrm{\dots },C_4$, where each coin starts at a known position. The agent uses one unit of fuel at each step, and cannot move if it has no fuel. It can get filled up (to 20 units of fuel) at the fuel station. In this case the state needs to take into account the position of the agent, the amount of fuel, and for each coin whether it has collected that coin. The state could be represented as the tuple

where $(x,y)$ is the position of the agent, $fuel$ is the amount of fuel the agent has, and $c_i$ is true when the agent has collected coin $C_i$. True is written as $t$ and false as $f$ here. The goal might be for the agent to have collected all coins and be at position $(1,1)$, which is the state

where ? means what the fuel is at the end does not matter. All states where the agent is at $(1,1)$ and all $c_i$ are true are goal states.

Part of the environment is shown in Figure 3.2(a), where the agent cannot move into a blacked-out square. It could get filled up at position $(4,9)$ and collect coin $C_3$ at position $(5,7)$.

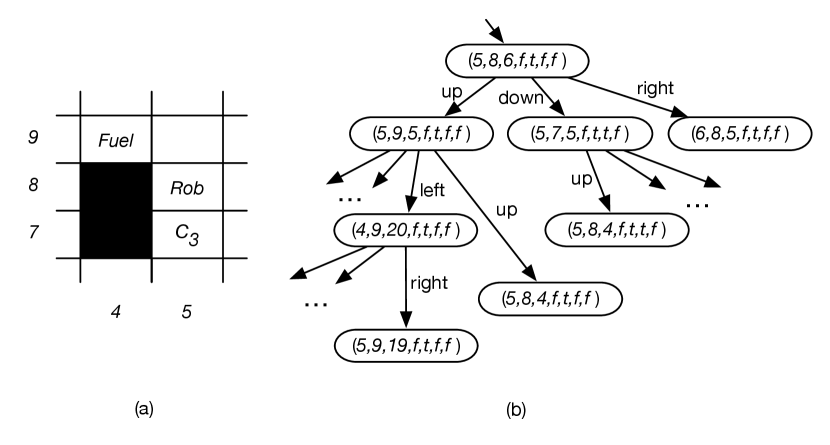
The state where the agent, Rob, is at position $(5,8)$ with 6 units of fuel, and has only collected coin $C_2$, is

Figure 3.2(b) shows part of the state space for this problem.

The delivery robot may have a number of parcels to deliver to various locations, where each parcel has its own delivery destination. In this case, the state may consist of the location of the robot, which parcels the robot is carrying, and the locations of the other parcels. The possible actions may be for the robot to move, to pick up parcels that are at the same location as the robot, or to put down some or all of the parcels it is carrying. A goal state may be one in which some specified parcels are at their delivery destination. There may be many goal states because where the robot is or where some of the other parcels are in a goal state does not matter.

Notice that this representation has ignored many details, for example, how the robot is carrying the parcels (which may affect whether it can carry other parcels), the battery level of the robot, whether the parcels are fragile or damaged, and the color of the floor. Not having these details as part of the state space implies that they are not relevant to the problem at hand.

In a simplified tutoring agent, a state may consist of the set of topics that the student knows, and the topics they have been introduced to, but do not know yet. The action may be teaching a lesson on a particular topic, with preconditions that the student knows any prerequisite topic, and the result that the student knows the topic of the lesson. The aim is for a student to know a particular set of topics.

If the effect of teaching also depends on the aptitude of the student, this detail must be part of the state space as well. The state does not need to include the items the student is carrying if what they are carrying does not affect the result of actions or whether the goal is achieved.