Artificial
Intelligence 2E
foundations of computational agents
The third edition of Artificial Intelligence: foundations of computational agents, Cambridge University Press, 2023 is now available (including full text).
9.3.1 Decision Networks
A decision network (also called an influence diagram) is a graphical representation of a finite sequential decision problem. Decision networks extend belief networks to include decision variables and utility. A decision network extends the single-stage decision network to allow for sequential decisions, and allows both chance nodes and decision nodes to be parents of decision nodes.
In particular, a decision network is a directed acyclic graph (DAG) with chance nodes (drawn as ovals), decision nodes (drawn as rectangles), and a utility node (drawn as a diamond). The meaning of the arcs is:
-
•
Arcs coming into decision nodes represent the information that will be available when the decision is made.
-
•
Arcs coming into chance nodes represent probabilistic dependence.
-
•
Arcs coming into the utility node represent what the utility depends on.

Example 9.13.
Figure 9.9 shows a simple decision network for a decision of whether the agent should take an umbrella when it goes out. The agent’s utility depends on the weather and whether it takes an umbrella. The agent does not get to observe the weather; it only observes the forecast. The forecast probabilistically depends on the weather.
As part of this network, the designer must specify the domain for each random variable and the domain for each decision variable. Suppose the random variable has domain , the random variable has domain , and the decision variable has domain . There is no domain associated with the utility node. The designer also must specify the probability of the random variables given their parents. Suppose is defined by
is given by
| Probability | ||
|---|---|---|
| 0.7 | ||
| 0.2 | ||
| 0.1 | ||
| 0.15 | ||
| 0.25 | ||
| 0.6 |
Suppose the utility function, , is
| 20 | ||
| 100 | ||
| 70 | ||
| 0 |
There is no table specified for the decision variable. It is the task of the planner to determine which value of to select, as a function of the forecast.
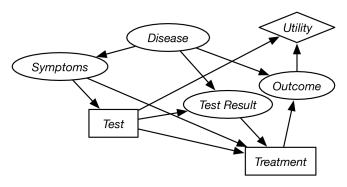
Example 9.14.
Figure 9.10 shows a decision network that represents the idealized diagnosis scenario of Example 9.12. The symptoms depend on the disease. What test to perform is decided based on the symptoms. The test result depends on the disease and the test performed. The treatment decision is based on the symptoms, the test performed, and the test result. The outcome depends on the disease and the treatment. The utility depends on the costs of the test and on the outcome.
The outcome does not depend on the test, but only on the disease and the treatment, so the test presumably does not have side effects. The treatment does not directly affect the utility; any cost of the treatment can be incorporated into the outcome. The utility needs to depend on the test unless all tests cost the same amount.
The diagnostic assistant that is deciding on the tests and the treatments never actually finds out what disease the patient has, unless the test result is definitive, which it, typically, is not.

Example 9.15.
Figure 9.11 gives a decision network that is an extension of the belief network of Figure 8.3. The agent can receive a report of people leaving a building and has to decide whether or not to call the fire department. Before calling, the agent can check for smoke, but this has some cost associated with it. The utility depends on whether it calls, whether there is a fire, and the cost associated with checking for smoke.
In this sequential decision problem, there are two decisions to be made. First, the agent must decide whether to check for smoke. The information that will be available when it makes this decision is whether there is a report of people leaving the building. Second, the agent must decide whether or not to call the fire department. When making this decision, the agent will know whether there was a report, whether it checked for smoke, and whether it can see smoke. Assume that all of the variables are binary.
The information necessary for the decision network includes the conditional probabilities of the belief network and
-
•
; how seeing smoke depends on whether the agent looks for smoke and whether there is smoke. Assume that the agent has a perfect sensor for smoke. It will see smoke if and only if it looks for smoke and there is smoke. See Exercise 9.
-
•
; how the utility depends on whether the agent checks for smoke, whether there is a fire, and whether the fire department is called. Figure 9.12 provides this utility information.
Figure 9.12: Utility for fire alarm decision network This utility function expresses the cost structure that calling has a cost of 200, checking has a cost of 20, but not calling when there is a fire has a cost of 5000. The utility is the negative of the cost.
A no-forgetting agent is an agent whose decisions are totally ordered in time, and the agent remembers its previous decisions and any information that was available to a previous decision.
A no-forgetting decision network is a decision network in which the decision nodes are totally ordered and, if decision node is before in the total ordering, then is a parent of , and any parent of is also a parent of .
Thus, any information available to is available to any subsequent decision, and the action chosen for decision is part of the information available for subsequent decisions. The no-forgetting condition is sufficient to make sure that the following definitions make sense and that the following algorithms work.


