Artificial
Intelligence 3E
foundations of computational agents
12.9 Exercises
Exercise 12.1.
Prove that the completeness and/or transitivity axioms, imply the following statements. What axiom(s) do your proofs rely on?
-
(a)
is equivalent to
-
(b)
-
(c)
-
(d)
.
Exercise 12.2.
Consider the following two alternatives:
-
(i)
In addition to what you currently own, you have been given $1000. You are now asked to choose one of these options:
50% chance to win $1000 or get $500 for sure.
-
(ii)
In addition to what you currently own, you have been given $2000. You are now asked to choose one of these options:
50% chance to lose $1000 or lose $500 for sure.
Explain how the predictions of utility theory and prospect theory differ for these alternatives.
Exercise 12.3.
One of the decisions we must make in real life is whether to accept an invitation even though we are not sure we can or want to go to an event. Figure 12.24 gives a decision network for such a problem.

Suppose that all of the decision and random variables are Boolean (i.e., have domain ). You can accept the invitation, but when the time comes, you still must decide whether or not to go. You might get sick in between accepting the invitation and having to decide to go. Even if you decide to go, if you have not accepted the invitation you may not be able to go. If you get sick, you have a good excuse not to go. Your utility depends on whether you accept, whether you have a good excuse, and whether you actually go.
-
(a)
Give a table representing a possible utility function. Assume the unique best outcome is that you accept the invitation, you do not have a good excuse, but you do go. The unique worst outcome is that you accept the invitation, you do not have a good excuse, and you do not go. Make your other utility values reasonable.
-
(b)
Suppose that you get to observe whether you are sick before accepting the invitation. Note that this is a different variable than if you are sick after accepting the invitation. Add to the network so that this situation can be modeled. You must not change the utility function, but the new observation must have a positive value of information. The resulting network must be no-forgetting.
-
(c)
Suppose that, after you have decided whether to accept the original invitation and before you decide to go, you can find out if you get a better invitation (to an event that clashes with the original event, so you cannot go to both). Suppose you would prefer the later invitation than the original event you were invited to. (The difficult decision is whether to accept the first invitation or wait until you get a better invitation, which you may not get.) Unfortunately, having another invitation does not provide a good excuse. On the network, add the node “better invitation” and all relevant arcs to model this situation. [You do not have to include the node and arcs from part (b).]
-
(d)
If you have an arc between “better invitation” and “accept invitation” in part (c), explain why (i.e., what must the world be like to make this arc appropriate). If you did not have such an arc, which way could it go to still fit the preceding story; explain what must happen in the world to make this arc appropriate.
-
(e)
If there was not an arc between “better invitation” and “accept invitation” (whether or not you drew such an arc), what must be true in the world to make this lack of arc appropriate?
Exercise 12.4.
Students have to make decisions about how much to study for each course. The aim of this question is to investigate how to use decision networks to help them make such decisions.
Suppose students first have to decide how much to study for the midterm. They can study a lot, study a little, or not study at all. Whether they pass the midterm depends on how much they study and on the difficulty of the course. As a rough approximation, they pass if they study hard or if the course is easy and they study a bit. After receiving their midterm grade, they have to decide how much to study for the final exam. The final exam result depends on how much they study and on the difficulty of the course. Their final grade (A, B, C, or F) depends on which exams they pass; generally they get an A if they pass both exams, a B if they only pass the final, a C if they only pass the midterm, or an F if they fail both. Of course, there is a great deal of noise in these general estimates.
Suppose that their utility depends on their subjective total effort and their final grade. Suppose their subjective total effort (a lot or a little) depends on their effort in studying for the midterm and the final.
-
(a)
Draw a decision network for a student decision based on the preceding story.
-
(b)
What is the domain of each variable?
-
(c)
Give appropriate conditional probability tables.
-
(d)
What is the best outcome (give this a utility of 100) and what is the worst outcome (give this a utility of 0)?
-
(e)
Give an appropriate utility function for a student who is lazy and just wants to pass (not get an F). The total effort here measures whether they (thought they) worked a lot or a little overall. Explain the best outcome and the worst outcome. Fill in a copy of the table of Table 12.4; use 100 for the best outcome and 0 for the worst outcome.
Grade Total Effort Utility A lot A little B lot B little C lot C little F lot F little Table 12.4: Utility function for the study decision -
(f)
Given your utility function for the previous part, give values for the missing terms for one example that reflects the utility function you gave above:
Comparing outcome
and lottery
when the outcome is preferred to the lottery
when the lottery is preferred to the outcome.
-
(g)
Give an appropriate utility function for a student who does not mind working hard and really wants to get an A, and would be very disappointed with a B or lower. Explain the best outcome and the worst outcome. Fill in a copy of the table of Table 12.4; use 100 for the best outcome and 0 for the worst outcome.
Exercise 12.5.
Some students choose to cheat on exams, and instructors want to make sure that cheating does not pay. A rational model would specify that the decision of whether to cheat depends on the costs and the benefits. Here we will develop and critique such a model.
Consider the decision network of Figure 12.25.
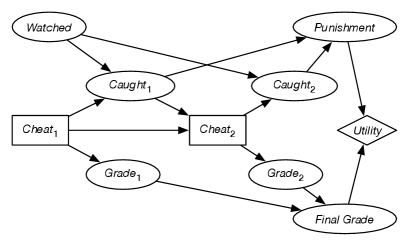
This diagram models a student’s decisions about whether to cheat at two different times. If students cheat they may be caught cheating, but they could also get higher grades. The punishment (either suspension, cheating recorded on the transcript, or none) depends on whether they get caught at either or both opportunities. Whether they get caught depends on whether they are being watched and whether they cheat. The utility depends on their final grades and their punishment.
The cheating decision network in AIPython (aipython.org) provides probabilities to use for the following questions.
-
(a)
What is an optimal policy? Give a description in English of an optimal policy. (The description should not use any jargon of AI or decision theory.) What is the value of an optimal policy?
-
(b)
What happens to the optimal policy when the probability of being watched goes up? [Modify the probability of “Watched”.] Try a number of values. Explain what happens and why.
-
(c)
What is an optimal policy when the rewards for cheating are reduced? Try a number of different parameterizations.
-
(d)
Change the model so that once students have been caught cheating, they will be watched more carefully. [Hint: Whether they are watched at the first opportunity needs to be a different variable than whether they are watched at the second opportunity.] Show the resulting model (both the structure and any new parameters), and give the policies and expected utilities for various settings of the parameters.
-
(e)
What does the current model imply about how cheating affects future grades? Change the model so that cheating affects subsequent grades. Explain how the new model achieves this.
-
(f)
How could this model be changed to be more realistic (but still be simple)? [For example: Are the probabilities reasonable? Are the utilities reasonable? Is the structure reasonable?]
-
(g)
Suppose the university decided to set up an honor system so that instructors do not actively check for cheating, but there is severe punishment for first offenses if cheating is discovered. How could this be modeled? Specify a model for this and explain what decision is optimal (for a few different parameter settings).
-
(h)
Should students and instructors be encouraged to think of the cheating problem as a rational decision in a game? Explain why or why not in a single paragraph.
Exercise 12.6.
Suppose that, in a decision network, the decision variable has parents and . Suppose you are using VE to find an optimal policy and, after eliminating all of the other variables, you are left with a single factor:
| 23 | |||
| 8 | |||
| 37 | |||
| 56 | |||
| 28 | |||
| 12 | |||
| 18 | |||
| 22 |
-
(a)
What is the resulting factor after eliminating ? [Hint: You do not sum out because it is a decision variable.]
-
(b)
What is the optimal decision function for ?
-
(c)
What is the value of information about for the decision for the decision network where is a parent of ? That is, if the agent has the information about , how much more is the information about worth?
Exercise 12.7.
Suppose that, in a decision network, there were arcs from random variables “contaminated specimen” and “positive test” to the decision variable “discard sample.” You solved the decision network and discovered that there was a unique optimal policy:
| Contaminated Specimen | Positive Test | Discard Sample |
|---|---|---|
What can you say about the value of information in this case?
Exercise 12.8.
How sensitive are the answers from the decision network of Example 12.16 to the probabilities? Test the program with different conditional probabilities and see what effect this has on the answers produced. Discuss the sensitivity both to the optimal policy and to the expected value of the optimal policy.
Exercise 12.9.
In Example 12.16, suppose that the fire sensor was noisy in that it had a false positive rate
and a false negative rate
Is it still worthwhile to check for smoke?
Exercise 12.10.
This exercise is to compare variable elimination and conditioning for the decision network of Example 12.16.
-
(a)
For the inverse of the variable ordering for search used in Example 12.20 (i.e., from to ) show the sequence of factors removed and created for variable elimination, in a table similar to Example 12.22 (only the variable ordering changes).
-
(b)
For the splitting order that is the inverse of the variable ordering of Example 12.22, specify what variables can be evaluated for each split (similar to Example 12.20, but with a different variable ordering. Also show what variables can be forgotten, as in Example 9.26.
-
(c)
How does the evaluation of the factors in recursive conditioning relate to the factors created for variable elimination, when the variable orderings are the inverse of each other? Be as specific as you can.
Exercise 12.11.
Consider the belief network of Exercise 9.10. When an alarm is observed, a decision is made whether or not to shut down the reactor. Shutting down the reactor has a cost associated with it (independent of whether the core was overheating), whereas not shutting down an overheated core incurs a cost that is much higher than .
-
(a)
Draw the decision network to model this decision problem for the original system (i.e., with only one sensor).
-
(b)
Specify the tables for all new factors that must be defined (you should use the parameters and where appropriate in the tables). Assume that utility is the negative of cost.
-
(c)
Show how variable elimination can be used to find the optimal decision. For each variable eliminated, show which variable is eliminated, how it is eliminated (through summing or maximization), which factors are removed, what factor is created, and what variables this factor is over (similar to Example 12.22). You are not required to give the tables.
Exercise 12.12.
Consider the following decision network:
![[Uncaptioned image]](x140.png)
-
(a)
What are the initial factors? (Give the variables in the scope of each factor, and specify any associated meaning of each factor.)
-
(b)
Give a legal splitting order, and the order that variables can be evaluated (similar to Example 12.20).
-
(c)
Show what factors are created in variable elimination when optimizing the decision function and computing the expected value, for one of the legal elimination orderings. At each step explain which variable is being eliminated, whether it is being summed out or maximized, what factors are being combined, and what factors are created (give the variables they depend on, not the tables).
-
(d)
If the value of information of at decision is zero, what does an optimal policy look like? (Give the most specific statement you can make about any optimal policy.)
Exercise 12.13.
What is the main difference between asynchronous value iteration and standard value iteration? Why does asynchronous value iteration often work better than standard value iteration?
Exercise 12.14.
Explain why we often use discounting of future rewards in MDPs. How would an agent act differently if the discount factor was 0.6 as opposed to 0.9?
Exercise 12.15.
Consider the MDP of Example 12.31.
-
(a)
As the discount varies between 0 and 1, how does the optimal policy change? Give an example of a discount that produces each different policy that can be obtained by varying the discount.
-
(b)
How can the MDP and/or discount be changed so that the optimal policy is to relax when healthy and to party when sick? Give an MDP that changes as few of the probabilities, rewards, or discount as possible to have this as the optimal policy.
-
(c)
The optimal policy computed in Example 12.33 was to party when healthy and relax when sick. What is the distribution of states that the agent following this policy will visit? [Hint: The policy induces a Markov chain, which has a stationary distribution.] What is the average reward of this policy? [Hint: The average reward can be obtained by computing the expected value of the immediate rewards with respect the stationary distribution.]
Exercise 12.16.
Consider a game world
![[Uncaptioned image]](x141.png)
The robot can be at any one of the 25 locations on the grid. There can be a treasure on one of the circles at the corners. When the robot reaches the corner where the treasure is, it collects a reward of 10, and the treasure disappears. When there is no treasure, at each time step, there is a probability that a treasure appears, and it appears with equal probability at each corner. The robot knows its position and the location of the treasure.
There are monsters at the squares marked with an . Each monster randomly and independently, at each time step, checks whether the robot is on its square. If the robot is on the square when the monster checks, it has a reward of (i.e., it loses 10 points). At the center point, the monster checks at each time step with probability ; at the other four squares marked with an , the monsters check at each time step with probability .
Assume that the rewards are immediate upon entering a state: that is, if the robot enters a state with a monster, it gets the (negative) reward on entering the state, and if the robot enters the state with a treasure, it gets the reward upon entering the state, even if the treasure arrives at the same time.
The robot has eight actions corresponding to the eight neighboring squares. The diagonal moves are noisy; there is a probability of going in the direction chosen and an equal chance of going to each of the four neighboring squares closest to the desired direction. The vertical and horizontal moves are also noisy; there is a chance of going in the requested direction and an equal chance of going to one of the adjacent diagonal squares. For example, the actions up-left and up have the following results:
![[Uncaptioned image]](x142.png)
If the action results in crashing into a wall, the robot has a reward of (i.e., loses 2) and does not move.
There is a discount factor of .
-
(a)
How many states are there? (Or how few states can you get away with?) What do they represent?
-
(b)
What is an optimal policy?
-
(c)
Suppose the game designer wants to design different instances of the game that have non-obvious optimal policies for a game player. Give three assignments to the parameters to with different optimal policies. If there are not that many different optimal policies, give as many as there are and explain why there are no more than that.
Exercise 12.17.
Consider a grid game similar to the game of the previous question. The agent can be at one of the 25 locations, and there can be a treasure at one of the corners or no treasure.
Assume the “up” action has same dynamics as in the previous question. That is, the agent goes up with probability 0.8 and goes up-left with probability 0.1 and up-right with probability 0.1.
If there is no treasure, a treasure can appear with probability 0.2. When it appears, it appears randomly at one of the corners, and each corner has an equal probability of treasure appearing. The treasure stays where it is until the agent lands on the square where the treasure is. When this occurs the agent gets an immediate reward of and the treasure disappears in the next state transition. The agent and the treasure move simultaneously so that if the agent arrives at a square at the same time the treasure appears, it gets the reward.
Suppose we are doing asynchronous value iteration and have the value for each state as in the following grids. The number in a square represent the value of that state and empty squares have a value of zero. It is irrelevant to this question how these values got there.
![[Uncaptioned image]](x143.png)
The left grid shows the values for the states where there is no treasure and the right grid shows the values of the states when there is a treasure at the top-right corner. There are also states for the treasures at the other three corners, but assume that the current values for these states are all zero.
Consider the next step of asynchronous value iteration. For state , which is marked by in the figure, and the action , which is “up,” what value is assigned to on the next value iteration? You must show all your work but do not have to do any arithmetic (i.e., leave it as an expression). Explain each term in your expression.
Exercise 12.18.
In a decision network, suppose that there are multiple utility nodes, where the values must be added. This lets us represent a generalized additive utility function. How can the VE for decision networks algorithm, shown in Figure 12.14, be altered to include such utilities?
Exercise 12.19.
How can variable elimination for decision networks, shown in Figure 12.14, be modified to include additive discounted rewards? That is, there can be multiple utility (reward) nodes, to be added and discounted. Assume that the variables to be eliminated are eliminated from the latest time step forward.



