Third edition of Artificial Intelligence: foundations of computational agents, Cambridge University Press, 2023 is now available (including the full text).
16.3 Relations and the Relational Algebra
Relations are common in AI and database systems. The relational algebra defines operations on relations and is the basis of relational databases.
A scope S is a set of variables. A tuple t on scope S, has a value on each variable in its scope. We write val(t,X) to be the value of tuple t on variable X. The value of val(t,X) must be in dom(X). This is like the mathematical notion of tuple, except the index is given by a variable, not by an integer.
A relation is a set of tuples, all with the same scope. A relation is often given a name. The scope of the tuples is often called the relation scheme. A relational database is a set of relations. A scheme of a relational database is the set of pairs of relation names and relation schemes.
A relation with scope X1,...,Xn can be seen as a Boolean factor on X1,...,Xn, where the true elements are represented as tuples.
Often a relation is written as a table.
| Course | Year | Student | Grade |
| cs322 | 2008 | fran | 77 |
| cs111 | 2009 | billie | 88 |
| cs111 | 2009 | jess | 78 |
| cs444 | 2008 | fran | 83 |
| cs322 | 2009 | jordan | 92 |
The heading gives the scheme, namely {Course, Year, Student, Grade}, and every other row is a tuple. The first tuple, call it t1 is defined by val(t1,Course)=cs322, val(t1,Year)=2008, val(t1,Student)=fran, val(t1,Grade)=77.
The order of the columns and the order of the rows is not significant.
If r a relation with scheme S, and c is a condition on the variables in S, the selection of c in r, written σc(r), is the set of tuples in r for which c holds. The selection has the same scheme as r.
If r is a relation with scheme S, and S0 ⊆S, the projection of r onto S0, written πS0(r), is the set of tuples of r where the scope is restricted to S0.
The relation σGrade > 79 (enrolled) selects those tuples in enrolled where the grade is over 79. This is the relation:
| Course | Year | Student | Grade |
| cs111 | 2009 | billie | 88 |
| cs444 | 2008 | fran | 83 |
| cs322 | 2009 | jordan | 92 |
The relation π{Student,Year}(enrolled) specifies what years students were enrolled:
| Student | Year |
| fran | 2008 |
| billie | 2009 |
| jess | 2009 |
| jordan | 2009 |
Notice how the first and the fourth tuple of enrolled become the same tuple in the projection; they represent the same function on {Student,Year}.
If two relations on the same scheme, the union, intersection and set difference of these are defined as the corresponding operations on the set of tuples.
If r1 and r2 are two relations, the natural join of
r1 and r2, written r1 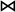 r2 is a
relation where
r2 is a
relation where
- the scheme of the join is the union of the scheme of r1 and the scheme of r2,
- a tuple is in the join, if the tuple restricted to the scope of r1 is in the relation r1 and the tuple restricted to the scope of r2 is in the relation r2.
| Course | Year | TA |
| cs322 | 2008 | yuki |
| cs111 | 2009 | sam |
| cs111 | 2009 | chris |
| cs322 | 2009 | yuki |
The join of enrolled and assisted, written enrolled 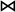 assisted is the relation:
assisted is the relation:
| Course | Year | Student | Grade | TA |
| cs322 | 2008 | fran | 77 | yuki |
| cs111 | 2009 | billie | 88 | sam |
| cs111 | 2009 | jess | 78 | sam |
| cs111 | 2009 | billie | 88 | chris |
| cs111 | 2009 | jess | 78 | chris |
| cs322 | 2009 | jordan | 92 | yuki |
Note how in the join, the information about cs444 was lost, as there was no TA in that course.



