Third edition of Artificial Intelligence: foundations of computational agents, Cambridge University Press, 2023 is now available (including the full text).
9.1 Preferences and Utility
What an agent decides to do should depend on its preferences. In this section, we specify some intuitive properties of preferences that we want and give a consequence of these properties. The properties that we give are axioms of rationality from which we prove a theorem about how to measure these preferences. You should consider whether each axiom is reasonable for a rational agent to follow; if you accept them all as reasonable, you should accept their consequence. If you do not accept the consequence, you should question which of the axioms you are willing to give up.
An agent chooses actions based on their outcomes. Outcomes are whatever the agent has preferences over. If the agent does not have preferences over anything, it does not matter what the agent does. Initially, we consider outcomes without considering the associated actions. Assume there are only a finite number of outcomes.
We define a preference relation over outcomes. Suppose o1 and o2 are outcomes. We say that o1 is weakly preferred to outcome o2, written o1 ≥o2, if outcome o1 is at least as desirable as outcome o2. The axioms that follow are arguably reasonable properties of such a preference relation.
Define o1 ∼o2 to mean o1 ≥o2 and o2 ≥o1. That is, o1 ∼o2 means outcomes o1 and o2 are equally preferred. In this case, we say that the agent is indifferent between o1 and o2.
Define o1 >o2 to mean o1 ≥o2 and ¬(o2 ≥o1). That is, the agent prefers outcome o1 to outcome o2 and is not indifferent between them. In this case, we say that o1 is strictly preferred to outcome o2.
Typically, an agent does not know the outcome of its actions. A lottery is defined to be a finite distribution over outcomes, written as
[p1:o1, p2:o2, ..., pk:ok],
where oi are outcomes and pi are non-negative real numbers such that
∑i pi = 1.
The lottery specifies that outcome oi occurs with probability pi. In all that follows, assume that outcomes include lotteries. This includes the case of having lotteries over lotteries.
∀o1 ∀o2 o1 ≥o2 or o2 ≥o1.
The rationale for this axiom is that an agent must act; if the actions available to it have outcomes o1 and o2 then, by acting, it is explicitly or implicitly preferring one outcome over the other.
if o1 ≥o2 and o2 ≥o3 then o1 ≥o3.
To see why this is reasonable, suppose it is false, in which case o1 ≥o2 and o2 ≥o3 and o3 >o1. Because o3 is strictly preferred to o1, the agent should be prepared to pay some amount to get from o1 to o3. Suppose the agent has outcome o3; then o2 is at least as good so the agent would just as soon have o2. o1 is at least as good as o2 so the agent would just as soon have o1 as o2. Once the agent has o1 it is again prepared to pay to get to o3. It has gone through a cycle of preferences and paid money to end up where it is. This cycle that involves paying money to go through it is known as a money pump because, by going through the loop enough times, the amount of money that agent must pay can exceed any finite amount. It seems reasonable to claim that being prepared to pay money to cycle through a set of outcomes is irrational; hence, a rational agent should have transitive preferences.
Also assume that monotonicity holds for mixes of > and ≥, so that if one or both of the preferences in the premise of the transitivity axiom is strict, then the conclusion is strict. That is, if o1 >o2 and o2 ≥o3 then o1 >o3. Also, if o1 ≥o2 and o2 >o3 then o1 >o3.
[p:o1, (1-p):o2] >[q:o1, (1-q):o2].
Note that, in this axiom, > between outcomes represents the agent's preference, whereas > between p and q represents the familiar comparison between numbers.
[p:o1, (1-p):[q:o2, (1-q):o3]] ∼[p:o1, (1-p)q: o2, (1-p)(1-q):o3].
Also o1 ∼[1:o1,0:o2] for any outcomes o1 and o2.
This axiom specifies that it is only the outcomes and their probabilities that define a lottery. If an agent had a preference for gambling, that would be part of the outcome space.
These axioms can be used to characterize much of an agent's preferences between outcomes and lotteries. Suppose that o1 >o2 and o2 >o3. Consider whether the agent would prefer
- o2 or
- the lottery [p:o1,(1-p):o3]
for different values of p ∈[0,1]. When p=1, the agent prefers the lottery (because the lottery is equivalent to o1 and o1 >o2). When p=0, the agent prefers o2 (because the lottery is equivalent to o3 and o2 >o3). At some stage, as p is varied, the agent's preferences flip between preferring o2 and preferring the lottery.
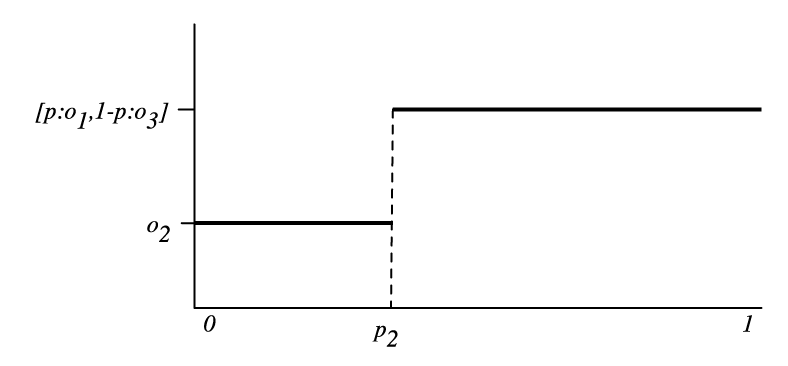
Figure 9.1 shows how the preferences must flip as p is varied. On the X-axis is p and the Y-axis shows which of o2 or the lottery is preferred.
- for all p<p2, the agent prefers o2 to the lottery (i.e., o2 >[p:o1,(1-p):o3]) and
- for all p>p2, the agent prefers the lottery (i.e., [p:o1,(1-p):o3] >o2).
The preceding proposition does not specify what the preference of the agent is at the point p2. The following axiom specifies that the agent is indifferent at this point.
o2 ∼[p2:o1,(1-p2):o3].
The next axiom specifies that, if you replace an outcome in a lottery with another outcome that is not worse, the lottery does not become worse.
[p:o1, (1-p):o3] ≥[p:o2, (1-p):o3].
A direct corollary of this is that you can substitutes outcomes for which the agent is indifferent and not change preferences:
[p:o1, (1-p):o3] ∼[p:o2, (1-p):o3].
This follows because o1 ∼o2 is equivalent to o1 ≥o2 and o2 ≥o1.
An agent is defined to be rational if it obeys the completeness, transitivity, monotonicity, decomposability, continuity, and substitutability axioms.
It is up to you to determine if this technical definition of rational matches your intuitive notion of rational. In the rest of this section, we show consequences of this definition.
Although preferences may seem to be very complicated, the following theorem shows that a rational agent's value for an outcome can be measured by a real number and that these numbers can be combined with probabilities so that preferences under uncertainty can be compared using expectation. This is surprising because
- it may seem that preferences are too multifaceted to be modeled by a single number. For example, although one may try to measure preferences in terms of dollars, not everything is for sale or easily converted into dollars and cents.
- you would not expect that values could be combined with probabilities. An agent that is indifferent between $(px+(1-p)y) and the lottery [p:$x, (1-p)$y] for all monetary values x and y and for all p∈[0,1] is known as an expected monetary value (EMV) agent. Most people are not EMV agents, because they have, for example, a strict preference between $1,000,000 and the lottery [0.5:$0,0.5:$2,000,000]. (Think about whether you would prefer a million dollars or a coin toss where you would get nothing if the coin lands heads or two million if the coin lands tails.) Money cannot be simply combined with probabilities, so it may be surprising that there is a value that can be.
- oi>oj if and only if u(oi) > u(oj) and
- utilities are linear with probabilities:
u([p1:o1, p2:o2, ..., pk:ok])=p1 u(o1)+ p2 u(o2)+ ...+ pk u(ok).
Otherwise, choose the best outcome, obest, and the worst outcome, oworst, and define, for any outcome o, the utility of o to be the value p such that
o ∼[p:obest, (1-p):oworst].
The first part of the proposition follows from substitutability and monotonicity.
The second part can be proved by replacing each oi by its equivalent lottery between obest and oworst. This composite lottery can be reduced to a single lottery between obest and oworst, with the utility given in the theorem. The details are left as an exercise.
In this proof the utilities are all in the range [0,1], but any linear scaling gives the same result. Sometimes [0,100] is a good scale to distinguish it from probabilities, and sometimes negative numbers are useful to use when the outcomes have costs. In general, a program should accept any scale that is intuitive to the user.
A linear relationship does not usually exist between money and utility, even when the outcomes have a monetary value. People often are risk averse when it comes to money. They would rather have $n in their hand than some randomized setup where they expect to receive $n but could possibly receive more or less.
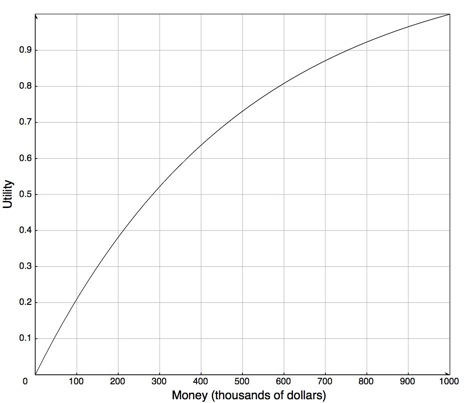
This agent would rather have $300,000 than a 50% chance of getting either nothing or $1,000,000, but would prefer the gamble on the million dollars to $275,000. They would also require more than a 73% chance of winning a million dollars to prefer this gamble to half a million dollars.
Note that, for this utility function, u($999000) approx 0.9997. Thus, given this utility function, the person would be willing to pay $1,000 to eliminate a 0.03% chance of losing all of their money. This is why insurance companies exist. By paying the insurance company, say $600, the agent can change the lottery that is worth $999,000 to them into one worth $1,000,000 and the insurance companies expect to pay out, on average, about $300, and so expect to make $300. The insurance company can get its expected value by insuring enough houses. It is good for both parties.
As presented here, rationality does not impose any conditions on what the utility function looks like.
Challenges to Expected Utility
There have been a number of challenges to the theory of expected utility. The Allais Paradox, presented in 1953 [Allais and Hagen (1979)], is as follows. Which would you prefer out of the following two alternatives?
- A:
- $1m - one million dollars
- B:
- lottery [0.10:$2.5m, 0.89:$1m, 0.01:$0]
Similarly, what would you choose between the following two alternatives?
- C:
- lottery [0.11:$1m,0.89:$0]
- D:
- lottery [0.10:$2.5m,0.9:$0]
It turns out that many people prefer A to B, and prefer D to C. This choice is inconsistent with the axioms of rationality. To see why, both choices can be put in the same form:
- A,C:
- lottery [0.11:$1m,0.89:X]
- B,D:
- lottery [0.10:$2.5m,0.01:$0,0.89:X]
In A and B, X is a million dollars. In C and D, X is zero dollars. Concentrating just on the parts of the alternatives that are different seems like an appropriate strategy, but people seem to have a preference for certainty.
Tversky and Kahneman (1974), in a series of human experiments, showed how people systematically deviate from utility theory. One such deviation is the framing effect of a problem's presentation. Consider the following:
- A disease is expected to kill 600 people. Two alternative programs
have been proposed:
- Program A:
- 200 people will be saved
- Program B:
- with probability 1/3, 600 people will be saved, and with probability 2/3, no one will be saved
Which program would you favor?
- A disease is expected to kill 600 people. Two alternative programs
have been proposed:
- Program C:
- 400 people will die
- Program D:
- with probability 1/3 no one will die, and with probability 2/3 600 will die
Which program would you favor?
Tversky and Kahneman showed that 72% of people in their experiments chose A over B, and 22% chose C over D. However, these are exactly the same choice, just described in a different way.
An alternative to expected utility is prospect theory, developed by Kahneman and Tversky, that takes into account an agent's current wealth at each time. That is, a decision is based on the agent's gains and losses, rather than the outcome. However, just because this better matches a human's choices does not mean it is the best for an artificial agent, but an artificial agent that must interact with humans should take into account how humans reason.



