Third edition of Artificial Intelligence: foundations of computational agents, Cambridge University Press, 2023 is now available (including the full text).
6.1.4 Expected Values
You can use the probabilities to give the expected value of any numerical random variable (i.e., one whose domain is a subset of the reals). A variable's expected value is the variable's weighted average value, where its value in each possible world is weighted by the measure of the possible world.
Suppose V is a random variable whose domain is numerical, and ω is a possible
world. Define V(ω) to be the value v in the domain
of V such that ω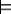 
V=v. That is, we are treating a
random variable as a function on worlds.
The expected value of numerical variable V, written E(V), is
E(V) = ∑ω∈ΩV(ω)×µ(ω)
when finitely many worlds exist. When infinitely many worlds exist, we must integrate.
E(number_of_broken_switches)
would give the expected number of broken switches. If the world acted according to the probability model, this would give the long-run average number of broken switches.
In a manner analogous to the semantic definition of conditional probability, the conditional expected value of variable X conditioned on evidence e, written E(V|e), is
E(V|e) = ∑ω∈ΩV(ω)×µe(ω).
Thus,
E(V|e) = (1)/(P(e))∑ω = ∑ω∈ΩV(ω)×P(ω|e ).
E(number_of_broken_switches|¬lit(l1)).
This is obtained by averaging the number of broken switches over all of the worlds in which light l1 is not lit.
