6 Deterministic Planning 6 Deterministic Planning 6.2 Forward Planning

6.1 Representing States, Actions, and Goals

To reason about what to do, assume an agent has goals, a model of the environment, and a model of its actions.

A deterministic action is a partial function from states to states. It is partial because not every action is able to be carried out in every state. For example, a robot cannot pick up a particular object if it is nowhere near the object. The precondition of an action specifies when the action can be carried out. The effect of an action specifies the resulting state.

Example 6.1.

Consider a delivery robot with mail and coffee to deliver. Assume a simplified problem domain with four locations as shown in Figure 6.1.

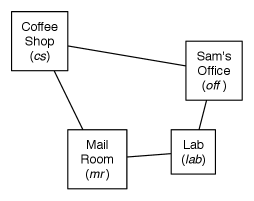
Refer to caption — Figure 6.1: The delivery robot domain

The robot, called Rob, can buy coffee at the coffee shop, pick up mail in the mail room, move, and deliver coffee and/or mail. Delivering the coffee to Sam’s office will stop Sam from wanting coffee. There could be mail waiting at the mail room to be delivered to Sam’s office. This domain is quite simple, yet it is rich enough to demonstrate many of the issues in representing actions and in planning.

The state is described in terms of the following features:

•

$R L o c$ , the robot’s location, which is one of the coffee shop ( $c s$ ), Sam’s office ( $o f f$ ), the mail room ( $m r$ ), or the laboratory ( $l a b$ ).
•

$R H C$ , whether the robot has coffee. The atom $r h c$ means Rob has coffee (i.e., $RHC{\,{=}\,}true$ ) and $\neg{rhc}$ means Rob does not have coffee (i.e., $RHC{\,{=}\,}false$ ).
•

$S W C$ , whether Sam wants coffee. The atom $s w c$ means Sam wants coffee and $\neg{swc}$ means Sam does not want coffee.
•

$M W$ , whether mail is waiting at the mail room. The atom $m w$ means there is mail waiting and $\neg{mw}$ means there is no mail waiting.
•

$R H M$ , whether the robot is carrying the mail. The atom $r h m$ means Rob has mail, and $\neg{rhm}$ means Rob does not have mail.

Rob has six actions:

•

Rob can move clockwise ( $m c$ ).
•

Rob can move counterclockwise ( $m c c$ ).
•

Rob can pick up coffee if Rob is at the coffee shop. Let $p u c$ mean that Rob picks up coffee. The precondition of $p u c$ is $\neg{rhc}\wedge RLoc{\,{=}\,}cs$ ; that is, Rob can pick up coffee in any state where its location is $c s$ , and it is not already holding coffee. The effect of this action is to make $R H C$ true. It does not affect the other features.
•

Rob can deliver coffee if Rob is carrying coffee and is at Sam’s office. Let $d c$ mean that Rob delivers coffee. The precondition of $d c$ is $rhc\wedge RLoc{\,{=}\,}off$ . The effect of this action is to make $R H C$ false and make $S W C$ false. Rob can deliver coffee whether or not Sam wants it.
•

Rob can pick up mail if Rob is at the mail room and there is mail waiting there. Let $p u m$ mean Rob picks up the mail.
•

Rob can deliver mail if Rob is carrying mail and at Sam’s office. Let $d m$ mean Rob delivers mail.

Assume that it is only possible for Rob to do one action at a time. We assume that a lower-level controller is able to implement these actions, as described in Chapter 2.

6.1.1 Explicit State-Space Representation

One possible representation of the effect and precondition of actions is to explicitly enumerate the states and, for each state, specify the actions that are possible in that state and, for each state–action pair, specify the state that results from carrying out the action in that state. This would require a table such as the following:

State	Action	Resulting State
$s_{7}$	$act_{47}$	$s_{94}$
$s_{7}$	$act_{14}$	$s_{83}$
$s_{94}$	$act_{5}$	$s_{33}$
…	…	…

The first tuple in this relation specifies that it is possible to carry out action $act_{47}$ in state $s_{7}$ and, if it were to be carried out in state $s_{7}$ , the resulting state would be $s_{94}$ .

Thus, this is the explicit representation of a graph, where the nodes are states and the acts are actions. This is a state-space graph. This is the sort of graph that was used in Chapter 3. Any of the algorithms of Chapter 3 can be used to search the space.

Example 6.2.

In Example 6.1, the states are the quintuples specifying the robot’s location, whether the robot has coffee, whether Sam wants coffee, whether mail is waiting, and whether the robot is carrying the mail. For example, the tuple

\left<lab,\neg{rhc},swc,\neg{mw},rhm\right>

represents the state where Rob is at the lab, Rob does not have coffee, Sam wants coffee, there is no mail waiting, and Sam has mail. The tuple

\left<lab,rhc,swc,mw,\neg{rhm}\right>

represents the state where Rob is at the lab carrying coffee, Sam wants coffee, there is mail waiting, and Rob is not holding any mail.

In this example, there are $4\times 2\times 2\times 2\times 2=64$ states. Intuitively, all of them are possible, even if one would not expect that some of them would be reached by an intelligent robot.

There are six actions, not all of which are applicable in each state.

The actions are defined in terms of the state transitions:

State	Action	Resulting State
$\left<lab,\neg{rhc},swc,\neg{mw},rhm\right>$	$m c$	$\left<mr,\neg{rhc},swc,\neg{mw},rhm\right>$
$\left<lab,\neg{rhc},swc,\neg{mw},rhm\right>$	$m c c$	$\left<off,\neg{rhc},swc,\neg{mw},rhm\right>$
$\left<off,\neg{rhc},swc,\neg{mw},rhm\right>$	$d m$	$\left<off,\neg{rhc},swc,\neg{mw},\neg{rhm}\right>$
$\left<off,\neg{rhc},swc,\neg{mw},rhm\right>$	$m c c$	$\left<cs,\neg{rhc},swc,\neg{mw},rhm\right>$
$\left<off,\neg{rhc},swc,\neg{mw},rhm\right>$	$m c$	$\left<lab,\neg{rhc},swc,\neg{mw},rhm\right>$
…	…	…

This table shows the transitions for two of the states. The complete representation includes the transitions for the other 62 states.

This is not a good representation for three main reasons:

•

There are usually too many states to represent, to acquire, and to reason with.
•

Small changes to the model mean a large change to the representation. Adding another feature means changing the whole representation. For example, to model the level of power in the robot, so that it can recharge itself in the lab, every state has to change.
•

It does not represent the structure of states; there is much structure and regularity in the effects of actions that is not reflected in the state transitions. For example, most actions do not affect whether Sam wants coffee, but this cannot be specified directly.

An alternative is to model how the actions affect the features.

6.1.2 The STRIPS Representation

The STRIPS representation is an action-centric representation which, for each action, specifies when the action can occur and the effects of the action. STRIPS, which stands for “STanford Research Institute Problem Solver,” was the planner used in Shakey, one of the first robots built using AI technology.

To represent a planning problem in STRIPS, first divide the features that describe the state of the world into primitive and derived features. The STRIPS representation is used to specify the values of primitive features in a state based on the previous state and the action taken by the agent. Definite clauses are used to determine the value of derived features from the values of the primitive features in any given state.

The STRIPS representation for an action consists of:

•

the precondition, a set of assignments of values to features that must hold for the action to occur
•

the effect, a set of assignments of values to primitive features that specifies the features that change, and the values they change to, as the result of the action.

The precondition of an action is a proposition – the conjunction of the elements of the set – that must be true before the action is able to be carried out. In terms of constraints, the robot is constrained so it can only choose an action for which the precondition holds.

Example 6.3.

In Example 6.1, the action of Rob to pick up coffee ( $p u c$ ) has precondition $\{cs,\neg{rhc}\}$ . That is, Rob must be at the coffee shop ( $c s$ ), not carrying coffee ( $\neg{rhc}$ ), to carry out the $p u c$ action. As a constraint, this means that $p u c$ is not available for any other location or when $r h c$ is true.

The action to move clockwise is always possible. Its precondition is the empty set, $\{\}$ , which represents the proposition $t r u e$ .

The STRIPS representation is based on the idea that most things are not affected by a single action. The semantics relies on the STRIPS assumption: the values of all of the primitive features not mentioned in the effects of the action are unchanged by the action.

Primitive feature $X$ has value $v$ after action $a c t$ if action $a c t$ is possible (its preconditions hold) and either

•

$X{\,{=}\,}v$ is in the effect of $a c t$ or
•

$X$ is not mentioned in the effect of $a c t$ and $X$ has value $v$ immediately before $a c t$ .

The values of non-primitive features can be derived from the values of the primitive features for each time.

Example 6.4.

In Example 6.1, the action of Rob to pick up coffee ( $p u c$ ) has the following STRIPS representation:

precondition: $\{cs,\neg{rhc}\}$
effect: $\{rhc\}$

That is, in order to be able to pick up coffee, the robot must be at the coffee shop and not have coffee. After the action, $r h c$ holds (i.e., $RHC{\,{=}\,}true$ ). All other feature values are unaffected by this action.

Example 6.5.

The action of delivering coffee ( $d c$ ) can be defined by

precondition: $\{off,rhc\}$
effect: $\{\neg{rhc},\neg{swc}\}$

The robot can deliver coffee when it is in the office and has coffee. The robot does not have coffee after the action, and Sam does not want coffee after the action. Thus, the effects are to make $RHC{\,{=}\,}false$ and $SWC{\,{=}\,}false$ . According to this model, the robot can deliver coffee whether or not Sam wants coffee. In either case, Sam does not want coffee immediately after the action.

STRIPS cannot directly define conditional effects, where the effect of an action depends on what is true initially. However, conditional effects can be modeled by introducing new actions, as shown in the following example.

Example 6.6.

Consider representing the action $m c$ to move clockwise. The effect of $m c$ , where the robot ends up, depends on the robot’s location before $m c$ was carried out.

To represent this in the STRIPS representation, we can construct multiple actions that differ in what is true initially. For example, the action $mc\_cs$ (move clockwise from coffee shop) has a precondition $\{RLoc{\,{=}\,}cs\}$ and effect $\{RLoc{\,{=}\,}off\}$ . The action $mc\_off$ (move clockwise from office) has a precondition $\{RLoc{\,{=}\,}off\}$ and effect $\{RLoc{\,{=}\,}lab\}$ . STRIPS thus requires four move clockwise actions (one for each location) and four move counterclockwise actions.

6.1.3 Feature-Based Representation of Actions

Whereas STRIPS is an action-centric representation, a feature-centric representation is more flexible, as it allows for conditional effects, and non-local effects.

A feature-based representation of actions models:

•

the precondition of each action
•

for each feature, the feature values in the next state as a function of the feature values of the previous state and the action.

The feature-based representation of actions uses definite clauses to specify the value of each variable in the state resulting from an action. The bodies of these rules can include propositions about the action carried out and propositions about values of features in the previous state. We assume these propositions can be equalities and inequalities between features and values.

The rules have two forms:

•

A causal rule specifies when a feature gets a new value.
•

A frame rule specifies when a feature keeps its value.

It is useful to think of these as two separate cases: what makes the feature change its value, and what makes it keep its value.

Example 6.7.

In Example 6.1, Rob’s location depends on its previous location and where it moved. Let $RLoc^{\prime}$ be the variable that specifies the location in the resulting state. The following rules specify the conditions under which Rob is at the coffee shop:

RLoc^{\prime}{\,{=}\,}cs\leftarrow\mbox{}RLoc{\,{=}\,}off\wedge\mbox{}Act{\,{=% }\,}mcc.

RLoc^{\prime}{\,{=}\,}cs\leftarrow\mbox{}RLoc{\,{=}\,}mr\wedge\mbox{}Act{\,{=}% \,}mc.

RLoc^{\prime}{\,{=}\,}cs\leftarrow\mbox{}RLoc{\,{=}\,}cs\wedge\mbox{}Act{\,{% \neq}\,}mcc\wedge\mbox{}Act{\,{\neq}\,}mc.

The first two rules are causal rules and the last rule is a frame rule.

Whether the robot has coffee in the resulting state depends on whether it has coffee in the previous state and its action. A causal rule specifies that picking up the coffee causes the robot to have coffee in the next time step:

rhc^{\prime}\leftarrow\mbox{}Act{\,{=}\,}puc.

A frame rule specifies that the robot having coffee persists unless the robot delivers the coffee:

rhc^{\prime}\leftarrow\mbox{}rhc\wedge\mbox{}Act{\,{\neq}\,}{dc}.

The rule implicitly implies that the robot cannot drop the coffee, drink it or lose it, and the coffee cannot be stolen.

The feature-based representation is more powerful than the STRIPS representation; it can represent anything representable in STRIPS, but can also represent conditional effects. It may be more verbose because it requires explicit frame axioms, which are implicit in the STRIPS representation.

The mapping from STRIPS to the feature-based representation for Boolean features is as follows. If the effect of an action $a c t$ is $\{e_{1},\dots,e_{k}\}$ , then the STRIPS representation is equivalent to the causal rules

e_{i}^{\prime}\leftarrow\mbox{}act.

for each $e_{i}$ that is made true by the action and the frame rules

c^{\prime}\leftarrow\mbox{}c\wedge\mbox{}act.

for each condition $c$ that does not involve a variable on the effects list. Thus each $e_{i}$ that assigns a feature to be false does not result in a rule. The precondition of each action is the same in both representations. Non-Boolean features may require multiple rules for the different values of the feature.

A conditional effect of an action depends on the value of other features. The feature-based representation is able to specify conditional effects, whereas STRIPS cannot represent these directly. Example 6.6 shows how to represent in STRIPS the action moving clockwise, where the effect depends on the previous state, by inventing new actions. Example 6.7 shows how the feature-based representation can represent actions without needing to invent those new actions by adding conditions to the rules. The feature-based representation also allows for non-local effects, as in the following example.

Example 6.8.

Suppose that all of the actions make the robot dirty, except for the $w a s h$ action that makes the robot clean. In STRIPS this would entail having dirty as an effect of every action. In the feature-based representation, we could add a rule that the robot is dirty after every action that is not $w a s h$ :

robot\_dirty^{\prime}\leftarrow Act{\,{\neq}\,}wash.

6.1.4 Initial States and Goals

In a typical planning problem, where the world is fully observable and deterministic, the initial state is defined by specifying the value for each feature for the initial state.

There are several different kinds of goals:

•

An achievement goal is a proposition that must be true in the final state.
•

A maintenance goal is a proposition that must be true in every state through which the agent passes. These are often safety goals – the goal of staying away from bad states.
•

A transient goal is a proposition that must be achieved somewhere in the plan.
•

A resource goal is the goal of minimizing some resource in the plan. For example, the goal may be to minimize fuel consumption or the time required to execute the plan.

In the rest of this chapter, we concentrate on achievement goals, where the goal is a set of assigned values to features, all of which must hold in the final state.

Artificial Intelligence 3E