3 Searching for Solutions

3.3 Graph Searching

In this chapter, the problem of finding a sequence of actions to achieve a goal is abstracted as searching for paths in directed graphs. Searching in graphs provides an appropriate abstract model of problem solving independent of a particular domain.

A directed graph consists of a set of nodes and a set of directed arcs between nodes. The idea is to find a path along these arcs from the start node to a goal node.

The abstraction is necessary because there may be more than one way to represent a problem as a graph. The examples in this chapter are in terms of state-space searching, where nodes represent states and arcs represent actions. Future chapters consider other ways to use graphs for problem solving.

3.3.1 Formalizing Graph Searching

A directed graph consists of:

  • •

    a set N of nodes

  • •

    a set A of arcs, where an arc is an ordered pair of nodes.

In this definition, a node could be anything. There may be infinitely many nodes and arcs. A graph need not be represented explicitly; only a procedure to generate nodes and arcs as needed is required.

The arc ⟨n1,n2⟩ is an outgoing arc from n1 and an incoming arc to n2.

A node n2 is a neighbor of n1 if there is an arc from n1 to n2; that is, if ⟨n1,n2⟩∈A. Note that being a neighbor does not imply symmetry; just because n2 is a neighbor of n1 does not imply that n1 is a neighbor of n2. Arcs may be labeled, for example, with the action that will take the agent from a node to its neighbor or with the cost of an action or both.

A path from node s to node g is a sequence of nodes ⟨n0,n1,…,nk⟩ such that s=n0, g=nk, and ⟨ni−1,ni⟩∈A; that is, there is an arc from ni−1 to ni for each i. Sometimes it is useful to view a path as the sequence of arcs, ⟨n0,n1⟩, ⟨n1,n2⟩,…, ⟨nk−1,nk⟩, or a sequence of labels of these arcs. Path ⟨n0,n1,…,ni⟩ is an initial part of ⟨n0,n1,…,nk⟩, when i≤k.

A goal is a Boolean function on nodes. Node n is a goal node if g⁢o⁢a⁢l⁢(n) is true.

To encode problems as graphs, one node is identified as the start node. A solution is a path from the start node to a goal node.

Sometimes there is a cost – a non-negative number – associated with arcs. The cost of arc ⟨ni,nj⟩ is written as c⁢o⁢s⁢t⁢(⟨ni,nj⟩).

The costs of arcs induce a cost of paths. Given a path p=⟨n0,n1,…,nk⟩, the cost of path p is the sum of the costs of the arcs in the path:

c⁢o⁢s⁢t⁢(p)=∑i=1kc⁢o⁢s⁢t⁢(⟨ni−1,ni⟩)=c⁢o⁢s⁢t⁢(⟨n0,n1⟩)+⋯+c⁢o⁢s⁢t⁢(⟨nk−1,nk⟩).

An optimal solution is one of the solutions that has the lowest cost. That is, an optimal solution is a path p from the start node to a goal node such that there is no path p′ from the start node to a goal node where c⁢o⁢s⁢t⁢(p′)<c⁢o⁢s⁢t⁢(p).

A state-space graph is a special type of graph where the nodes are the states, and there is an arc ⟨ni,nj⟩ if there is an action that is possible to be carried out in ni and the effect of the action is to be in state nj. Future chapters consider other ways to represent problems as graphs.

Example 3.6.

Consider the problem of the delivery robot finding a path from location A to location G in the domain shown in Figure 3.1. The nodes are the labelled locations. Assume that the robot is only able to travel in one direction between the locations. Figure 3.3 shows the resulting graph where the nodes represent locations and the arcs represent possible single steps between locations. Each arc is shown with its associated cost, an estimate of the travel time of getting from one location to the next.

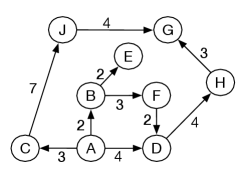
Refer to caption
Figure 3.3: A graph with arc costs for the delivery domain of Figure 3.1

In this graph, the set of nodes is {A,B,C,D,E,F,G,H,J} and the set of arcs is {⟨A,B⟩,⟨A,C⟩,⟨A,D⟩,⟨B,E⟩,…}. Node E has no neighbors. Node B has two neighbors, namely E and F. A is not a neighbor of B as there is no arc from B to A.

There are three paths from A to G:

⟨A,B,F,D,H,G⟩⟨A,D,H,G⟩⟨A,C,J,G⟩

If A were the start node and G were the unique goal node, all three paths would be a solution to the graph-searching problem. The second, with cost 4+4+3=11, is an optimal solution.

A cycle is a non-empty path where the end node is the same as the start node – that is, ⟨n0,n1,…,nk⟩ such that n0=nk. A directed graph without any cycles is called a directed acyclic graph (DAG). Note that this should be called an acyclic directed graph, because it is a directed graph that happens to be acyclic, not an acyclic graph that happens to be directed, but DAG sounds better than ADG! The graph of Figure 3.3 is a DAG.

A tree is a DAG where there is one node with no incoming arcs and every other node has exactly one incoming arc. The node with no incoming arcs is called the root of the tree. A node with no outgoing arcs is called a leaf. In a tree, an arc goes from a parent to a child; the family-tree metaphor, with grandparents, siblings, and so on, is often used.

In many problems the search graph is not given explicitly, but is dynamically constructed as needed. For the search algorithms, all that is required is a way to generate the neighbors of a node and to determine if a node is a goal node.

The forward branching factor of a node is the number of outgoing arcs from the node. The backward branching factor of a node is the number of incoming arcs to the node. These factors provide measures for the complexity of graph algorithms. In the time and space complexity discussed below, assume that the branching factors are bounded, meaning they are all less than some positive integer.

Example 3.7.

In the graph of Figure 3.3, the forward branching factor of node A is three because there are three outgoing arcs from node A. The backward branching factor of node A is zero; there are no incoming arcs to node A. The forward branching factor of E is zero and the backward branching factor of E is one. The forward branching factor of node B is two and the backward branching factor of B is one.

The branching factor is an important key component in the size of the graph. If the forward branching factor for each node is b, and the graph is a tree, there are bn nodes that are n arcs away from any node. (This is only possible if the tree is infinite.)