4 Reasoning with Constraints 4.2 Solving CSPs by Searching 4.4 Domain Splitting

4.3 Consistency Algorithms

Although depth-first search over the search space of assignments is usually a substantial improvement over generate and test, it still has various inefficiencies that can be overcome.

Example 4.13.

In Example 4.12, the variables $A$ and $B$ are related by the constraint $A<B$ . The assignment $A{\,{=}\,}4$ is inconsistent with each of the possible assignments to $B$ because $dom(B)=\{1,2,3,4\}$ . In the course of the backtrack search (see Figure 4.2), this fact is rediscovered for different assignments to $B$ and $C$ . This inefficiency can be avoided by the simple expedient of deleting $4$ from $dom(A)$ , once and for all. This idea is the basis for the consistency algorithms.

The consistency algorithms are best thought of as operating over a constraint network defined as:

•

There is a node (drawn as a circle or an oval) for each variable.
•

There is a node (drawn as a rectangle) for each constraint.
•

For every constraint $c$ , and for every variable $X$ in the scope of $c$ , there is an arc $\left<X,c\right>$ . The constraint network is thus a bipartite graph, with the two parts consisting of the variable nodes and the constraint nodes; each arc goes from a variable node to a constraint node.
•

There is also a dictionary $d o m$ with the variables as keys, where $dom[X]$ is a set of possible values for variable $X$ . $dom[X]$ is initially the domain of $X$ .

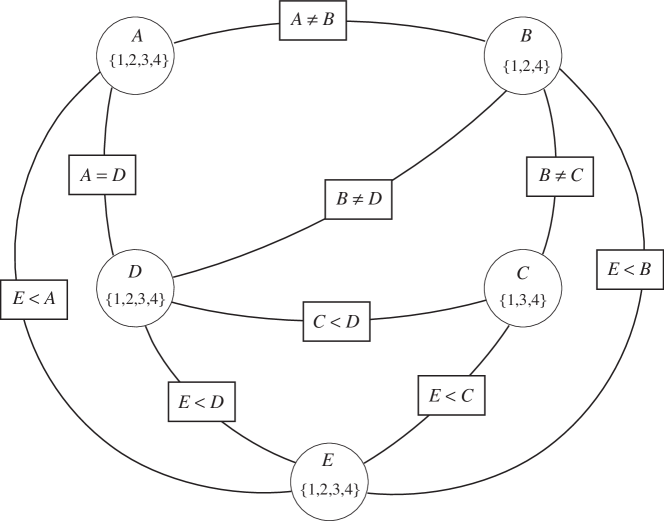
Refer to caption — Figure 4.3: Constraint network for the CSP of Example 4.14

Example 4.14.

Consider Example 4.12. There are three variables $A$ , $B$ , and $C$ , each with domain $\{1,2,3,4\}$ . The constraints are $A<B$ and $B<C$ . In the constraint network, shown in Figure 4.3, there are four arcs:

\left<A,A<B\right>

\left<B,A<B\right>

\left<B,B<C\right>

\left<C,B<C\right>.

Example 4.15.

The constraint $X\neq 4$ has one arc:

\left<X,X\neq 4\right>.

The constraint $X+Y=Z$ has three arcs:

\left<X,X+Y=Z\right>

\left<Y,X+Y=Z\right>

\left<Z,X+Y=Z\right>.

In the simplest case, when a constraint has just one variable in its scope, the arc is domain consistent if every value of the variable satisfies the constraint.

Example 4.16.

The constraint $B\neq 3$ has scope $\{B\}$ . With this constraint, and with $dom[B]=\{1,2,3,4\}$ , the arc $\left<B,B\neq 3\right>$ is not domain consistent because $B{\,{=}\,}3$ violates the constraint. If the value 3 were removed from the domain of $B$ , then it would be domain consistent.

Suppose constraint $c$ has scope $\{X,Y_{1},\dots,Y_{k}\}$ . Arc $\left<X,c\right>$ is arc consistent if, for each value $x\in dom[X]$ , there are values $y_{1},\dots,y_{k}$ where $y_{i}\in dom[Y_{i}]$ , such that the assignment $\{X{\,{=}\,}x,Y_{1}{\,{=}\,}y_{1},\dots,Y_{k}{\,{=}\,}y_{k}\}$ satisfies $c$ . A network is arc consistent if all its arcs are arc consistent.

Example 4.17.

Consider the network of Example 4.14 shown in Figure 4.3. None of the arcs are arc consistent. The first arc, $\left<A,A<B\right>$ , is not arc consistent because for $A{\,{=}\,}4$ there is no corresponding value for $B$ for which $A<B$ . If $4$ were removed from the domain of $A$ , then it would be arc consistent. The second arc, $\left<B,A<B\right>$ , is not arc consistent because there is no corresponding value for $A$ when $B{\,{=}\,}1$ .

If an arc $\left<X,c\right>$ is not arc consistent, there are some values of $X$ for which there are no values for $Y_{1},\dots,Y_{k}$ for which the constraint holds. In this case, all values of $X$ in $dom[X]$ for which there are no corresponding values for the other variables can be deleted from $dom[X]$ to make the arc $\left<X,c\right>$ consistent. When a value is removed from a domain, this may make some other arcs that were previously consistent no longer consistent.

1: procedure GAC(

{Vs},{dom},{Cs},{to\_do}

)

2: while

{to\_do}\neq\{\}

3: select and remove

\left<X,c\right>

from

{to\_do}

4: let

\{Y_{1},\dots,Y_{k}\}={scope}(c)\setminus\{X\}

{ND}\;{:}{=}\;\mbox{}\{x\mid x\in{dom}[X]

and exists

y_{1}\in{dom}[Y_{1}]\dots y_{k}\in{dom}[Y_{k}]

6: such that

c(X{\,{=}\,}x,Y_{1}{\,{=}\,}y_{1},\dots,Y_{k}{\,{=}\,}y_{k})\}

7: if

{ND}\neq{dom}[X]

then

{to\_do}\;{:}{=}\;\mbox{}{to\_do}\cup\{\left<Z,c^{\prime}\right>\mid\{X,Z\}% \subseteq{scope}(c^{\prime})

c^{\prime}\neq c

Z\neq X\}

{dom}[X]\;{:}{=}\;\mbox{}{ND}

10: return

{dom}

Figure 4.4: Generalized arc consistency algorithm. Returns arc-consistent domains for CSP

\left<{Vs},{dom},{Cs}\right>

given

{to\_do}

The generalized arc consistency (GAC) algorithm is given in Figure 4.4. It takes in a CSP with variables $V s$ , constraints $C s$ , and (possibly reduced) domains specified by the dictionary ${dom}$ and a set ${to\_do}$ of potentially inconsistent arcs. The set ${to\_do}$ initially consists of all arcs in the graph, $\{\left<X,c\right>\mid c\in{Cs}\mbox{ and }X\in{scope}(c)\}$ . It modifies ${dom}$ to make the network arc consistent.

While ${to\_do}$ is not empty, an arc $\left<X,c\right>$ is removed from the set and considered. If the arc is not arc consistent, it is made arc consistent by pruning the domain of variable $X$ . All of the previously consistent arcs that could, as a result of pruning $X$ , have become inconsistent are added to the set ${to\_do}$ if they are not already there. These are the arcs $\left<Z,c^{\prime}\right>$ , where $c^{\prime}$ is a constraint different from $c$ that involves $X$ , and $Z$ is a variable involved in $c^{\prime}$ other than $X$ . When ${to\_do}$ is empty, the constraint graph is arc consistent.

Example 4.18.

Consider the ${GAC}$ algorithm operating on the network from Example 4.14, with constraints $A<B$ , $B<C$ . Initially, all of the arcs are in the ${to\_do}$ set. Here is one possible sequence of selections of arcs, showing what values are pruned and what is added to the set $to\_do$ .

Arc	Domain reduced	Added to $to\_do$
$\left<A,A<B\right>$	$dom[A]=\{1,2,3\}$	–
$\left<B,A<B\right>$	$dom[B]=\{2,3,4\}$	–
$\left<B,B<C\right>$	$dom[B]=\{2,3\}$	$\left<A,A<B\right>$
$\left<A,A<B\right>$	$dom[A]=\{1,2\}$	–
$\left<C,B<C\right>$	$dom[C]=\{3,4\}$	–

In the first step, the algorithm selects the arc $\left<A,A<B\right>$ . For $A{\,{=}\,}4$ , there is no value of $B$ that satisfies the constraint. Thus, $4$ is pruned from the domain of $A$ . Nothing is added to ${to\_do}$ because there is no arc involving $B$ not in ${to\_do}$ .

In the second step, $1$ is removed from the domain of $B$ . The arc $\left<A,A<B\right>$ is not added back to ${to\_do}$ because it involves the same constraint as the arc visited.

In the third step, $\left<B,B<C\right>$ is selected. The value $4$ is removed from the domain of $B$ . Because the domain of $B$ has been reduced, the arc $\left<A,A<B\right>$ must be added back into the ${to\_do}$ set because the domain of $A$ could potentially be reduced further now that the domain of $B$ is smaller.

The algorithm then terminates with $dom[A]=\{1,2\}$ , $dom[B]=\{2,3\}$ , $dom[C]=\{3,4\}$ . Although this has not fully solved the problem, it has greatly simplified it. For example, depth-first backtracking search would now solve the problem more efficiently.

Example 4.19.

Consider applying ${GAC}$ to the scheduling problem of Example 4.9. The network shown in Figure 4.5 has already been made domain consistent (the value 3 has been removed from the domain of $B$ and $2$ has been removed from the domain of $C$ ).

The following is a sequence of arcs processed for one sequence of selections from $to\_do$ , where the order of arcs is arbitrary:

Arc	Domain Reduced	Added to $to\_do$
$\left<B,B\neq C\right>$	–	–
$\left<D,C<D\right>$	$dom[D]=\{2,3,4\}$	–
$\left<C,E<C\right>$	$dom[C]=\{3,4\}$	$\left<D,C<D\right>$ , $\left<B,B\neq C\right>$
$\left<D,C<D\right>$	$dom[D]=\{4\}$	–
$\left<B,B\neq C\right>$	–	–
$\left<C,C<D\right>$	$dom[C]=\{3\}$	$\left<B,B\neq C\right>$
$\left<A,A=D\right>$	$dom[A]=\{4\}$	–
$\left<B,B\neq D\right>$	$dom[B]=\{1,2\}$	–
$\left<B,E<B\right>$	$dom[B]=\{2\}$	$\left<B,B\neq D\right>$
$\left<E,E<B\right>$	$dom[E]=\{1\}$	$\left<C,E<C\right>$
…	–	–

At the end, all the arcs are consistent, and so the algorithm terminates with the ${to\_do}$ set empty. The set of reduced variable domains is returned. In this case, the domains all have size 1 and there is a unique solution: $A{\,{=}\,}4$ , $B{\,{=}\,}2$ , $C{\,{=}\,}3$ , $D{\,{=}\,}4$ , $E{\,{=}\,}1$ .

Notice that at the third step, when $C$ is reduced, all processed constraints that involve $C$ , but do not involve $E$ , are added back to the set $to\_do$ .

Regardless of the order in which the arcs are considered, the algorithm will terminate with the same result, namely, an arc-consistent network and the same set of reduced domains. Three cases are possible, depending on the state of the network upon termination:

•

In the first case, one domain becomes empty, indicating there is no solution for the CSP. Note that, as soon as any one domain becomes empty, all domains of connected nodes will become empty before the algorithm terminates.
•

In the second case, each domain has a singleton value, indicating that there is a unique solution, as in Example 4.19.
•

In the third case, every domain is non-empty and at least one has multiple values. There may or may not be a solution. Methods to solve the problem in this case are explored in the following sections.

The following example shows that it is possible for a network to be arc consistent even though there is no solution.

Example 4.20.

Suppose there are variables, $A$ , $B$ , and $C$ , each with the domain $\{1,2,3,4\}$ and constraints $A=B$ , $B=C$ , and $A\neq C$ . This is arc consistent: no domain can be pruned using any single constraint. However, there are no solutions; there is no assignment to the three variables that satisfies the constraints.

Consider the time complexity of the generalized arc-consistency algorithm for binary constraints. Suppose there are $c$ binary constraints, and the domain of each variable is of size $d$ . There are $2c$ arcs. Checking an arc $\left<X,r(X,Y)\right>$ involves, in the worst case, iterating through each value in the domain of $Y$ for each value in the domain of $X$ , which takes $O(d^{2})$ time. This arc may need to be checked once for every element in the domain of $Y$ , thus GAC for binary variables can be done in time $O(cd^{3})$ , which is linear in $c$ , the number of constraints. The space used is $O(nd)$ , where $n$ is the number of variables and $d$ is the domain size. Exercise 4.5 explores the complexity of more general constraints.

Various extensions to arc consistency are also possible. The domains need not be finite; they may be specified using intensions, such as $3<X<7$ . Higher-order consistency techniques, such as path consistency, consider $k$ -tuples of variables at a time, not just pairs of variables that are connected by a constraint. For example, by considering all three variables, an algorithm could recognize that there is no solution in Example 4.20. These higher-order methods are often less efficient for solving a problem than using arc consistency augmented with the methods described below.

Artificial Intelligence 3E