Artificial
Intelligence 3E
foundations of computational agents
4.12 Exercises
Exercise 4.1.
Consider the crossword puzzle shown in Figure 4.14.

Words:
add, age, aid, aim, air, are,
arm, art, bad, bat, bee, boa, dim, ear, eel, eft, lee, oaf
You must find six three-letter words: three words read across (1-across, 4-across, 5-across) and three words read down (1-down, 2-down, 3-down). Each word must be chosen from the list of 18 possible words shown. Try to solve it yourself, first by intuition, then using domain consistency, and then arc consistency.
There are at least two ways to represent the crossword puzzle shown in Figure 4.14 as a constraint satisfaction problem.
The first is to represent the word positions (1-across, 4-across, etc.) as variables, with the set of words as possible values. The constraints are that the letter is the same where the words intersect.
The second is to represent the nine squares as variables. The domain of each variable is the set of letters of the alphabet, . The constraints are that there is a word in the word list that contains the corresponding letters. For example, the top-left square and the center-top square cannot both have the value , because there is no word starting with .
-
(a)
Give an example of pruning due to domain consistency using the first representation (if one exists).
-
(b)
Give an example of pruning due to arc consistency using the first representation (if one exists).
-
(c)
Are domain consistency plus arc consistency adequate to solve this problem using the first representation? Explain.
-
(d)
Give an example of pruning due to domain consistency using the second representation (if one exists).
-
(e)
Give an example of pruning due to arc consistency using the second representation (if one exists).
-
(f)
Are domain consistency plus arc consistency adequate to solve this problem using the second representation?
-
(g)
Which representation leads to a more efficient solution using consistency-based techniques? Give the evidence on which you are basing your answer.
Exercise 4.2.
Suppose you have a relation that is true if there is a vowel (one o: a, e, i, o, u) as the -th letter of word . For example, is true because there is a vowel (“a”) as the second letter of the word “cat”; is false because the third letter of “cat” is “t”, which is not a vowel; and is also false because there is no fifth letter in “cat”.
Suppose the domain of is and the domain of is added, blue, fever, green, stare.
-
(a)
Is the arc arc consistent? If so, explain why. If not, show what element(s) can be removed from a domain to make it arc consistent.
-
(b)
Is the arc arc consistent? If so, explain why. If not, show what element(s) can be removed from a domain to make it arc consistent.
Exercise 4.3.
Consider the crossword puzzles shown in Figure 4.15.


(a) (b)
The possible words for (a) are
ant, big, bus, car, has, book, buys, hold, lane, year, ginger, search, symbol, syntax.
The available words for (b) are
at, eta, be, hat, he, her, it, him, on, one, desk, dance, usage, easy, dove, first, else, loses, fuels, help, haste, given, kind, sense, soon, sound, this, think.
-
(a)
Draw the constraint graph nodes for the positions (1-across, 2-down, etc.) and words for the domains, after it has been made domain consistent.
-
(b)
Give an example of pruning due to arc consistency.
-
(c)
What are the domains after arc consistency has halted?
-
(d)
Consider the dual representation in which the squares on the intersection of words are the variables. The domains of the variable contain the letters that could go in those positions. Give the domains after this network has been made arc consistent. Does the result after arc consistency in this representation correspond to the result in part (c)?
-
(e)
Show how variable elimination solves the crossword problem. Start from the arc-consistent network from part (c).
-
(f)
Does a different elimination ordering affect the efficiency? Explain.
Exercise 4.4.
Pose and solve the crypt-arithmetic problem as a CSP. In a crypt-arithmetic problem, each letter represents a different digit, the leftmost digit cannot be zero (because then it would not be there), and the sum must be correct considering each sequence of letters as a base ten numeral. In this example, you know that and that , and so on.
Exercise 4.5.
Consider the complexity for generalized arc consistency beyond the binary case considered in the text. Suppose there are variables, constraints, where each constraint involves variables, and the domain of each variable is of size . How many arcs are there? What is the worst-case cost of checking one arc as a function of , , and ? How many times must an arc be checked? Based on this, what is the time complexity of GAC as a function of , , and ? What is the space complexity?
Exercise 4.6.
For the constraints of Example 4.9, shown in Figure 4.5, show the variables eliminated, the constraints joined, and the new constraint (as in Example 4.23) for the variable ordering elimination ordering , , , .
Exercise 4.7.
Consider how stochastic local search can solve Exercise 4.3. You can use the AIPython (aipython.org) code to answer this question. Start with the arc-consistent network.
-
(a)
How well does random walking work?
-
(b)
How well does iterative best improvement work?
-
(c)
How well does the combination work?
-
(d)
Which (range of) parameter settings works best? What evidence did you use to answer this question?
Exercise 4.8.
Consider a scheduling problem, where there are five activities to be scheduled in four time slots. Suppose we represent the activities by the variables , , , , and , where the domain of each variable is and the constraints are , , , , , , , and . [Before you start this, try to find the legal schedule(s) using your own intuitions.]
-
(a)
Show how backtracking solves this problem. To do this, you should draw the search tree generated to find all answers. Indicate clearly the valid schedule(s). Make sure you choose a reasonable variable ordering.
To indicate the search tree, write it in text form with each branch on one line. For example, suppose we had variables , , and with domains , and constraints and . The corresponding search tree is written as
X=t Y=t failure Y=f Z=t solution Z=f failure X=f Y=t Z=t failure Z=f solution Y=f failure[Hint: It may be easier to write a program to generate such a tree for a particular problem than to do it by hand.]
-
(b)
Show how arc consistency solves this problem. To do this you must
-
–
draw the constraint graph
-
–
show which arc is considered, the domain reduced, and the arcs added to the set (similar to the table of Example 4.18)
-
–
show explicitly the constraint graph after arc consistency has stopped
-
–
show how splitting a domain can be used to solve this problem.
-
–
Exercise 4.9.
Which of the following methods can
-
(a)
determine that there is no model, if there is not one
-
(b)
find a model if one exists
-
(c)
find all models?
The methods to consider are
-
(i)
arc consistency with domain splitting
-
(ii)
variable elimination
-
(iii)
stochastic local search
-
(iv)
genetic algorithms.
Exercise 4.10.
Give the algorithm for variable elimination to return one of the models rather than all of them. How is finding one easier than finding all?

Exercise 4.11.
Consider the constraint network in Figure 4.16. The form of the constraints are not given, but assume the network is arc consistent and there are multiple values for each variable. Suppose one of the search algorithms has split on variable , so is assigned the value .
-
(a)
Suppose the aim is to count the number of solutions. Bao suggested that the subproblem with can be divided into two that can be solved separately. How can the solutions to each half be combined?
-
(b)
Suppose the constraints are soft constraints (with costs for each assignment). Manpreet suggested that the problem with can be divided into two subproblems that can be solved separately, with the solution combined. What are the two independent subproblems? How can the optimal solution (the cost and the total assignment) be computed from a solution to each subproblem?
-
(c)
How can the partitioning of constraints into non-empty sets such that the constraints in each set do not share a non-assigned variable (the sets that can be solved independently) be implemented?
Exercise 4.12.
Explain how arc consistency with domain splitting can be used to count the number of models. If domain splitting results in a disconnected graph, how can this be exploited by the algorithm?
Exercise 4.13.
Modify to count the number of models, without enumerating them all. [Hint: You do not need to save the join of all the constraints, but instead you can pass forward the number of solutions there would be.]
Exercise 4.14.
Consider the constraint graph of Figure 4.17 with named binary constraints. is a relation on and , which we write as , and similarly for the other relations. Consider solving this network using variable elimination.
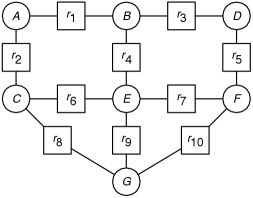
-
(a)
Suppose you were to eliminate variable . Which constraints are removed? A constraint is created on which variables? (You can call this .)
-
(b)
Suppose you were to subsequently eliminate (i.e., after eliminating ). Which relations are removed? A constraint is created on which variables?



