• Exercise 11.1.

  Suppose Kim has a camper van (a mobile home) and likes to keep it at a comfortable temperature and noticed that the energy use depended on the elevation. Kim knows that the elevation affects the outside temperature. Kim likes the camper warmer at higher elevation. Note that not all of the variables directly affect electrical usage.

  • (a)

    Show how this can be represented as a causal network, using the variables Elevation, Electrical Usage, Outside Temperature, and Thermostat Setting.

  • (b)

    Give an example where intervening has an effect different from conditioning for this network.

  Exercise 11.2.

  Exercise 9.2 asked to intuitively explore independence in Figure 9.37. For parts (c), (d), and (e) of Exercise 9.2, express the question in terms of conditional independence, and use d-separation to infer the answer. Show your working.

  Exercise 11.3.

  

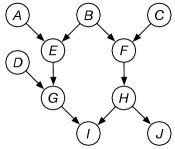
  Consider the causal network of Figure 11.12. For each part, explain why the independence holds or doesn’t hold, using the definition of d-separation. The independence asked needs to hold for all probability distributions (which is what d-separation tells us).

  • (a)

    Is $J$ independent of $A$ given $\{\}$ (i.e., given no observations)?

  • (b)

    Is $J$ independent of $A$ given $\{G\}$ (i.e., given only $G$ is observed)?

  • (c)

    Is $J$ independent of $A$ given $\{F\}$?

  • (d)

    Is $J$ independent of $A$ given $\{G,F\}$ (i.e., given only $G$ and $F$ are observed)?

  • (e)

    Is $G$ independent of $J$ given $\{\}$?

  • (f)

    Is $G$ independent of $J$ given $\{I\}$?

  • (g)

    Is $G$ independent of $J$ given $\{B\}$?

  • (h)

    Is $G$ independent of $J$ given $\{B,I\}$?

  • (i)

    What needs to be observed, and what needs to be not observed for $G$ to be independent of $J$? Give a complete characterization.

Consider the causal network of Figure 11.12. The following can be answered intuitively or using the do-calculus. Explain your reasoning:

• (a)

  Does $P(I\mid B)=P(I\mid do(B))$?

• (b)

  Does $P(I\mid G)=P(J\mid do(G))$?

• (c)

  Does $P(I\mid G,B)=P(J\mid do(G),B)$?

• (d)

  Does $P(B\mid I)=P(B\mid do(I))$?

Bickel et al. [1975] report on gender biases for graduate admissions at UC Berkeley. This example is based on that case, but the numbers are fictional.

There are two departments, which we will call $dept\mathrm{\#}1$ and $dept\mathrm{\#}2$ (so $Dept$ is a random variable with values $dept\mathrm{\#}1$ and $dept\mathrm{\#}2$), which students can apply to. Assume students apply to one, but not both. Students have a gender (male or female), and are either admitted or not. Consider the table of the percent of students in each category of Figure 11.13.

In the semantics of possible worlds, we will treat the students as possible worlds, with the measure of a set of worlds corresponding to the number of students in the set.

• (a)

  What is $P(Admitted=true\mid Gender=male)$?
  What is $P(Admitted=true\mid Gender=female)$?
  Which gender is more likely to be admitted?

• (b)

  What is $P(Admitted=true\mid Gender=male,Dept=dept\mathrm{\#}1)$?
  What is $P(Admitted=true\mid Gender=female,Dept=dept\mathrm{\#}1)$?
  Which gender is more likely to be admitted to $dept\mathrm{\#}1$?

• (c)

  What is $P(Admitted=true\mid Gender=male,Dept=dept\mathrm{\#}2)$?
  What is $P(Admitted=true\mid Gender=female,Dept=dept\mathrm{\#}2)$?
  Which gender is more likely to be admitted to $dept\mathrm{\#}2$?

• (d)

  This is an instance of Simpson’s paradox. Why is it a paradox? Explain why it happened in this case.

• (e)

  Does this provide evidence that the university has a bias against women? See Section 11.3.4.

• (f)

  Give another scenario where Simpson’s paradox occurs.

Suppose someone provided the source code for a recursive conditioning program that computes conditional probabilities in belief networks. Your job is to use it to build a program that also works for interventions, that is for queries of the form $P(Y\mid do(a_1,\mathrm{\dots },a_k),b_1,\mathrm{\dots },b_m)$. Explain how you would proceed.

Consider a two-variable causal network with Boolean variables $A$ and $B$, where $A$ is a parent of $B$, and the following conditional probabilities:

Consider the counterfactual: “$B$ is observed to be true; what is the probability of $B$ if $A$ was false?”

Draw the belief network that can be used to answer this question. Give all (conditional) probabilities. What needs to be conditioned on and what is queried to answer this counterfactual question? What is the resulting answer? (This can be done by hand or using any belief network implementation.)