Artificial
Intelligence 2E
foundations of computational agents
The third edition of Artificial Intelligence: foundations of computational agents, Cambridge University Press, 2023 is now available (including full text).
8.5.4 Dynamic Belief Networks
The state at a particular time need not be represented as a single variable. It is often more natural to represent the state in terms of features.
A dynamic belief network (DBN) is a discrete time belief network with regular repeated structure. It is like a (hidden) Markov model, but the states and the observations are represented in terms of features. If is a feature, we write as the random variable that represented the value of variable at time . A dynamic belief network makes the following assumptions:
-
•
The set of features is the same at each time.
-
•
For any time , the parents of variable are variables at time or time , such that the graph for any time is acyclic. The structure does not depend on the value of (except is a special case).
-
•
The conditional probability distribution of how each variable depends on its parents is the same for every time . This is called a stationary model.
Thus, a dynamic belief network specifies a belief network for time , and for each variable specifies , where the parents of are in the same or previous time steps. This is specified for as a free parameter; the conditional probabilities can be used for any time . As in a belief network, directed cycles are not allowed.
The model for a dynamic belief network is represented as a two-step belief network, which represents the variables at the first two times (times 0 and 1). That is, for each feature there are two variables, and . The set of parents of , namely can only include variables for time 0. The resulting graph must be acyclic. Associated with the network are the probabilities and .
The two-step belief network is unfolded into a belief network by replicating the structure for subsequent times. In the unfolded network, , for , has exactly the same structure and the same conditional probability values as .
Example 8.34.
Suppose a trading agent wants to model the dynamics of the price of a commodity such as printer paper. To represent this domain, the designer models variables affecting the price and the other variables. Suppose the cost of pulp and the transportation costs directly affect the price of paper. The transportation costs are affected by the weather. The pulp cost is affected by the prevalence of tree pests, which in turn depend on the weather. Suppose that each variable depends on its value at the previous time step. A two-stage dynamic belief network representing these dependencies is shown in Figure 8.17.
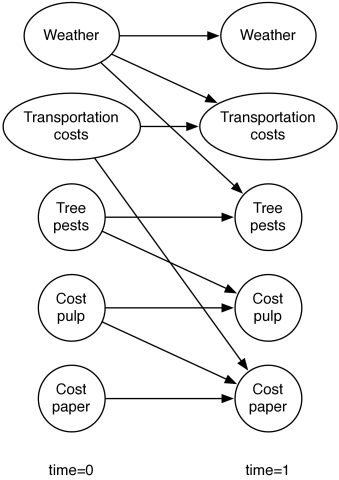
According to this figure, the variables are initially independent.
This two-stage dynamic belief network can be expanded into a regular dynamic belief network by replicating the nodes for each time step, and the parents for future steps are a copy of the parents for the time 1 variables.
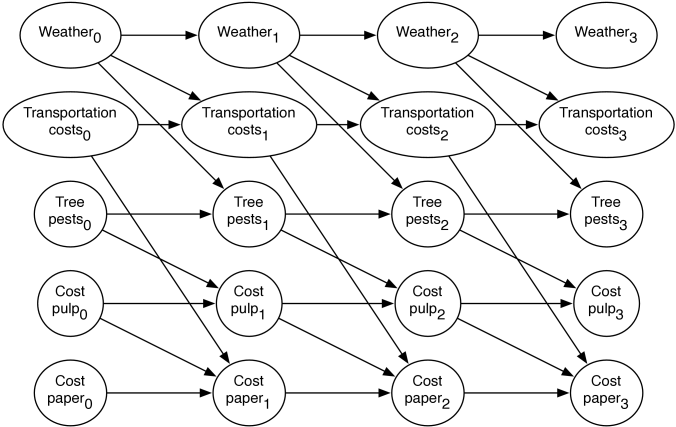
An expanded belief network for a horizon of 3 is shown in Figure 8.18. The subscripts represent the time that the variable is referring to.


