Third edition of Artificial Intelligence: foundations of computational agents, Cambridge University Press, 2023 is now available (including the full text).

5.1.2 Semantics of the Propositional Calculus

Semantics specifies how to put symbols of the language into correspondence with the world. Semantics can be used to understand sentences of the language. The semantics of propositional calculus is defined below.

An interpretation consists of a function π that maps atoms to {true, false}. If π(a)=true, we say atom a is true in the interpretation, or that the interpretation assigns true to a. If π(a)=false, we say a is false in the interpretation. Sometimes it is useful to think of π as the set of atoms that map to true, and that the rest of the atoms map to false.

The interpretation maps each proposition to a truth value. Each proposition is either true in the interpretation or false in the interpretation. An atomic proposition a is true in the interpretation if π(a)=true; otherwise, it is false in the interpretation. The truth value of a compound proposition is built using the truth table of Figure 5.1.

Note that we only talk about the truth value in an interpretation. Propositions may have different truth values in different interpretations.

p q ¬p p ∧q p∨q p ←q p →q p ↔q
true true false true true true true true
true false false false true true falsefalse
false true true false true false true false
false false true false false true true true
Figure 5.1: Truth table defining ¬, ∧, ∨, ←, →, and ↔
Example 5.1: Suppose there are three atoms: ai_is_fun, happy, and light_on.

Suppose interpretation I1 assigns true to ai_is_fun, false to happy, and true to light_on. That is, I1 is defined by the function π1 defined by π1(ai_is_fun)=true, π1(happy)=false, and π1(light_on)=true. Then

  • ai_is_fun is true in I1.
  • ¬ai_is_fun is false in I1.
  • happy is false in I1.
  • ¬happy is true in I1.
  • ai_is_fun∨happy is true in I1.
  • ai_is_fun ←happy is true in I1.
  • happy ←ai_is_fun is false in I1.
  • ai_is_fun ←happy ∧light_on is true in I1.

Suppose interpretation I2 assigns false to ai_is_fun, true to happy, and false to light_on:

  • ai_is_fun is false in I2.
  • ¬ai_is_fun is true in I2.
  • happy is true in I2.
  • ¬happy is false in I2.
  • ai_is_fun∨happy is true in I2.
  • ai_is_fun ←happy is false in I2.
  • ai_is_fun ←light_on is true in I2.
  • ai_is_fun ←happy ∧light_on is true in I2.

A knowledge base is a set of propositions that the agent is given as being true. An element of the knowledge base is an axiom.

A model of a set of propositions is an interpretation in which all the propositions are true.

If KB is a knowledge base and g is a proposition, g is a logical consequence of KB, written as

KB |= g

if g is true in every model of KB.

That is, no interpretation exists in which KB is true and g is false. The definition of logical consequence places no constraints on the truth value of g in an interpretation where KB is false.

If KB 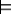|= g we also say g logically follows from KB, or KB entails g.

Example 5.2: Suppose KB is the following knowledge base:
sam_is_happy.
ai_is_fun.
worms_live_underground.
night_time.
bird_eats_apple.
apple_is_eaten ←bird_eats_apple.
switch_1_is_up ←sam_is_in_room ∧night_time.

Given this knowledge base,

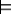KB |= bird_eats_apple.
KB 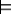|= apple_is_eaten.

KB does not entail switch_1_is_up as there is a model of the knowledge base where switch_1_is_up is false. Note that sam_is_in_room must be false in that interpretation.