Artificial
Intelligence 3E
foundations of computational agents
5.3 Propositional Definite Clauses
The rest of this chapter considers some restricted languages and reasoning tasks that are useful and can be efficiently implemented.
The language of propositional definite clauses is a subset of propositional calculus that does not allow uncertainty or ambiguity. In this language, propositions have the same meaning as in propositional calculus, but not all compound propositions are allowed in a knowledge base.
The syntax of propositional definite clauses is defined as follows:
-
•
An atomic proposition or atom is the same as in propositional calculus.
-
•
A definite clause is of the form
where is an atom, the head of the clause, and each is an atom. It can be read “ if and …and ”.
If , the clause is called a rule, where is the body of the clause.
If , the arrow can be omitted and the clause is called an atomic clause or fact. The clause has an empty body.
-
•
A knowledge base is a set of definite clauses.
Example 5.7.
The elements of the knowledge base in Example 5.2 are all definite clauses.
The following are not definite clauses:
The fourth statement is not a definite clause because an atom must start with a lower-case letter.
A definite clause is false in interpretation if are all true in and is false in ; otherwise, the definite clause is true in .
A definite clause is a restricted form of a clause. For example, the definite clause
is equivalent to the clause
In general, a definite clause is equivalent to a clause with exactly one positive literal (non-negated atom). Propositional definite clauses cannot represent disjunctions of atoms (e.g., ) or disjunctions of negated atoms (e.g., ).
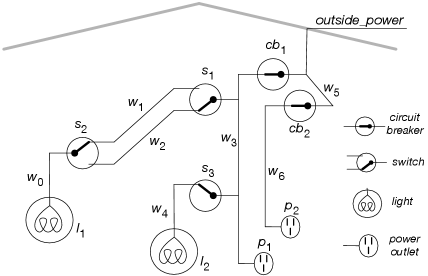
Example 5.8.
Consider how to axiomatize the electrical environment of Figure 5.2 following the methodology for the user’s view of semantics. This axiomatization will allow us to simulate the electrical system. It will be expanded in later sections to let us diagnose faults based on observed symptoms.
The representation will be used to determine whether lights are on or off, based on switch positions and the status of circuit breakers.
The knowledge base designer must choose a level of abstraction. The aim is to represent the domain at the most general level that will enable the agent to solve the problems it must solve. We also want to represent the domain at a level that the agent will have information about. For example, we could represent the actual voltages and currents, but exactly the same reasoning would be done if this were a 12-volt DC system or a 120-volt AC system; the voltages and frequencies are irrelevant for questions about how switch positions (up or down) affect whether lights are on. Our agent is not concerned here with the color of the wires, the design of the switches, the length or weight of the wire, the date of manufacture of the lights and the wires, or any of the other myriad details one could imagine about the domain.
Let’s represent this domain at a commonsense level that non-electricians may use to describe the domain, in terms of wires being live and currents flowing from the outside through wires to the lights, and that circuit breakers and light switches connect wires if they are turned on and working.
The designer must choose what to represent. Here we represent propositions about whether lights are lit, whether wires are live, whether switches are up or down, and whether components are working properly.
We then choose atoms with a specific meaning in the world. We can use descriptive names for these. For example, is true when switch is up. is true when light is working properly (will be lit if it is has power coming into it). is true when has power coming in. The computer does not know the meaning of these names and does not have access to the components of the atom’s name.
At this stage, we have not told the computer anything. It does not know what the atoms are, let alone what they mean.
Once we have decided which symbols to use and what they mean, we tell the system, using definite clauses, background knowledge about what is true in the world. The simplest forms of definite clauses are those without bodies – the atomic clauses – such as
The designer may look at part of the domain and know that light is live if wire is live, because they are connected together, but may not know whether is live. Such knowledge is expressible in terms of rules:
Online, the user is able to input the observations of the current switch positions, such as
The knowledge base consists of all the definite clauses, whether specified as background knowledge or as observations.
5.3.1 Queries and Answers
One reason to build a description of a real or imaginary world is to be able to determine what else must be true in that world. After the computer is given a knowledge base about a particular domain, a user might like to ask the computer questions about that domain. The computer can answer whether or not a proposition is a logical consequence of the knowledge base. A user that knows the meaning of the atoms, for example when is true, can interpret the answer in terms of the domain.
A query is a way of asking whether a proposition is a logical consequence of a knowledge base. Once the system has been provided with a knowledge base, a query is used to ask whether a proposition is a logical consequence of the knowledge base. Queries have the form
where is an atom or a conjunction of atoms (analogous to the body of a rule).
A query is a question that has the answer yes if the body is a logical consequence of the knowledge base, or the answer no if the body is not a consequence of the knowledge base. The latter does not mean that is false in the intended interpretation but rather that it is impossible to determine whether it is true or false based on the knowledge provided.
Example 5.9.
Once the computer has been told the knowledge base of Example 5.8, it can answer queries such as
for which the answer is yes. The query
has answer no. The computer does not have enough information to know whether or not is a light. The query
has answer yes. This atom is true in all models.
The user can interpret this answer with respect to the intended interpretation.
5.3.2 Proofs
So far, we have specified what an answer is, but not how it can be computed. The definition of specifies which propositions should be logical consequences of a knowledge base but not how to compute them. The problem of deduction is to determine if some proposition is a logical consequence of a knowledge base. Deduction is a specific form of inference.
A proof is a mechanically derivable demonstration that a proposition logically follows from a knowledge base. A theorem is a provable proposition. A proof procedure is a – possibly non-deterministic – algorithm for deriving consequences of a knowledge base. (See the box for a description of non-deterministic choice.)
Given a proof procedure, means can be proved or derived from knowledge base .
A proof procedure’s quality can be judged by whether it computes what it is meant to compute.
A proof procedure is sound with respect to the semantics if everything that can be derived from a knowledge base is a logical consequence of the knowledge base. That is, if , then .
A proof procedure is complete with respect to the semantics if there is a proof of each logical consequence of the knowledge base. That is, if , then .
We present two ways to construct proofs for propositional definite clauses: a bottom-up procedure and a top-down procedure.
Bottom-Up Proof Procedure
A bottom-up proof procedure can be used to derive all logical consequences of a knowledge base. It is called bottom-up as an analogy to building a house, where each part of the house is built on the structure already completed. The bottom-up proof procedure builds on atoms that have already been established. It should be contrasted with a top-down approach, which starts from a query and tries to find definite clauses that can be used to prove the query. Sometimes we say that a bottom-up procedure is forward chaining on the definite clauses, in the sense of going forward from what is known rather than going backward from the query.
The general idea is based on one rule of derivation, a generalized form of the rule of inference called modus ponens:
If “” is a definite clause in the knowledge base, and each has been derived, then can be derived.
An atomic clause corresponds to the case of ; modus ponens can always immediately derive any atomic clauses in the knowledge base.
Figure 5.3 gives a procedure for computing the consequence set of a set of definite clauses. Under this proof procedure, if is an atom, if at the end of the procedure. For a conjunction, , if .
Example 5.10.
Given the knowledge base :
one trace of the value assigned to in the bottom-up procedure is
The algorithm terminates with . Thus, , , and so on.
The last rule in is never used. The bottom-up proof procedure cannot derive or . This is as it should be because there is a model of the knowledge base in which and are both false.
The proof procedure of Figure 5.3 has a number of interesting properties:
- Soundness
-
The bottom-up proof procedure is sound. Every atom in is a logical consequence of . That is, if then . To show this, assume that there is an atom in that is not a logical consequence of . If such an atom exists, let be the first atom added to that is not true in every model of . Suppose is a model of in which is false. Because has been generated, there must be some definite clause in of the form such that are all in (which includes the case where is an atomic clause and so ). Because is the first atom added to that is not true in all models of , and the are generated before , all of the are true in . This clause’s head is false in , and its body is true in . Therefore, by the definition of truth of clauses, this clause is false in . This is a contradiction to the fact that is a model of . Thus, every element of is a logical consequence of .
- Complexity
-
The algorithm of Figure 5.3 halts, and the number of times the loop is repeated is bounded by the number of definite clauses in . This is easily seen because each definite clause is only used at most once. Thus, the time complexity of the bottom-up proof procedure is linear in the size of the knowledge base if it indexes the definite clauses so that the inner loop is carried out in constant time.
- Fixed Point
-
The final generated in the algorithm of Figure 5.3 is called a fixed point because any further application of the rule of derivation does not change . is the least fixed point because there is no smaller fixed point.
Let be the interpretation in which every atom in the least fixed point is true and every atom not in the least fixed point is false. To show that must be a model of , suppose “ is false in . The only way this could occur is if are in the fixed point, and is not in the fixed point. By construction, the rule of derivation can be used to add to the fixed point, a contradiction to it being the fixed point. Therefore, there can be no definite clause in that is false in an interpretation defined by a fixed point. Thus, is a model of .
is the minimal model in the sense that it has the fewest true propositions. Every other model must also assign the atoms in to be true.
- Completeness
-
The bottom-up proof procedure is sound. Suppose . Then is true in every model of , so it is true in the minimal model, and so it is in , and so .
Top-Down Proof Procedure
An alternative proof method is to search backwards or top-down from a query to determine whether it is a logical consequence of the given definite clauses. This procedure is called propositional definite clause resolution or SLD resolution, where SL stands for Selecting an atom using a Linear strategy and D stands for Definite clauses. It is an instance of the more general resolution method.
The top-down proof procedure can be understood as refining an answer clause of the form
where is a special atom. Intuitively, is going to be true exactly when the answer to the query is “yes.”
If the query is
then the initial answer clause is
Given an answer clause , the top-down algorithm selects an atom in the body of the answer clause. Suppose it selects the leftmost atom, . The atom selected is called a subgoal. The algorithm proceeds by doing steps of resolution. In one step of resolution, it chooses a definite clause in with as the head. If there is no such clause, the algorithm fails.
Suppose the chosen clause is .
The resolvent of the answer clause with the definite clause is the answer clause
That is, an atom is replaced by the body of a definite clause with that atom in the head.
An answer is an answer clause with an empty body (). That is, it is the answer clause .
An SLD derivation of a query “” from knowledge base is a sequence of answer clauses such that:
-
•
is the answer clause corresponding to the original query, namely the answer clause
-
•
is the resolvent of with a definite clause in
-
•
is an answer.
Another way to think about the algorithm is that the top-down algorithm maintains a collection (list or set) of atoms to prove. Each atom that must be proved is a subgoal. Initially, contains the atoms in the query. A clause means can be replaced by . The query is proved when becomes empty.
Figure 5.4 specifies a non-deterministic procedure for solving a query. It follows the definition of a derivation. In this procedure, is the set of atoms in the body of the answer clause. The procedure is non-deterministic: at line 12 it has to choose a definite clause to resolve against. If there are choices that result in being the empty set, the algorithm returns ; otherwise it fails, and the answer is .
This algorithm treats the body of a clause as a set of atoms and is also a set of atoms. An alternative, used by the language Prolog, is to have as a list of atoms, in which case duplicates are not eliminated, as they would be if were a set. In Prolog, the order of the atoms is defined by the programmer. It does not have the overhead of checking for duplicates, which is needed for maintaining a set.
Example 5.11.
The following shows a derivation that corresponds to a sequence of assignments to in the repeat loop of Figure 5.4, where the leftmost atom in the body is selected:
The following shows a sequence of choices, where the second definite clause for was chosen. This choice does not lead to a proof.
If is selected, there are no rules that can be chosen. This proof attempt is said to fail.
Note the use of select and choose (see box). Any atom in the body can be selected, and if one selection does not lead to a proof, other selections do not need to be tried. When choosing a clause, the algorithm may need to search for a choice that makes the proof succeed. Given a selection strategy, the algorithm induces a search graph. Each node in the search graph represents an answer clause. The neighbors of a node , where is the selected atom, represent all of the possible answer clauses obtained by resolving on . There is a neighbor for each definite clause whose head is . The goal nodes of the search are of the form .
Example 5.12.
Given the knowledge base
and the query
the search graph for an SLD derivation, assuming the leftmost atom is selected in each answer clause, is shown in Figure 5.5.
The search graph is not defined statically, because this would require anticipating every possible query. Instead, the search graph is dynamically constructed as needed.
Any of the search methods of Chapter 3 can be used to search the search space. The search space depends on the query and which atom is selected at each node. Whether the query is a logical consequence does not depend on the path found, so an optimal path is not necessary.
When the top-down procedure has derived the answer, the rules used in the derivation can be used in a bottom-up proof procedure to infer the query. Similarly, a bottom-up proof of an atom can be used to construct a corresponding top-down derivation. This equivalence can be used to show the soundness and completeness of the top-down proof procedure. As defined, the top-down proof procedure may spend extra time re-proving the same atom multiple times, whereas the bottom-up procedure proves each atom only once. However, the bottom-up procedure proves every atom, but the top-down procedure proves only atoms that are relevant to the query.
It is possible that the proof procedure can get into an infinite loop, as in the following example (without cycle pruning).
Example 5.13.
Consider the knowledge base
Atoms and are the only atomic logical consequences of this knowledge base, and the bottom-up proof procedure will halt with fixed point . However, the top-down proof procedure with a depth-first search, trying to prove , will go on indefinitely, and not halt if the first clause for is chosen, and there is no cycle pruning.
The algorithm requires a selection strategy to decide which atom to select at each time. In the above examples the leftmost atom was selected, but any atom could be selected. Which atom is selected affects the efficiency and perhaps even whether the algorithm terminates if there is no cycle pruning. The best selection strategy is to select the atom that is most likely to fail. Ordering the atoms and selecting the leftmost atom is a common strategy, because this lets someone who is providing the rules provide heuristic knowledge about which atom to select.



