Artificial
Intelligence 3E
foundations of computational agents
15.2 Symbols and Semantics
The basic idea behind the use of logic (see Chapter 5) is that, when knowledge base designers have a particular world they want to characterize, they can select that world as an intended interpretation, select meanings for the symbols with respect to that interpretation, and write, as axioms, what is true in that world. When a system computes a logical consequence of a knowledge base, a user that knows the meanings of the symbols can interpret this answer with respect to the intended interpretation. Because the intended interpretation is a model, and a logical consequence is true in all models, a logical consequence must be true in the intended interpretation. This chapter expands the propositional logic to allow reasoning about individuals and relations. Atomic propositions now have internal structure in terms of relations and individuals.
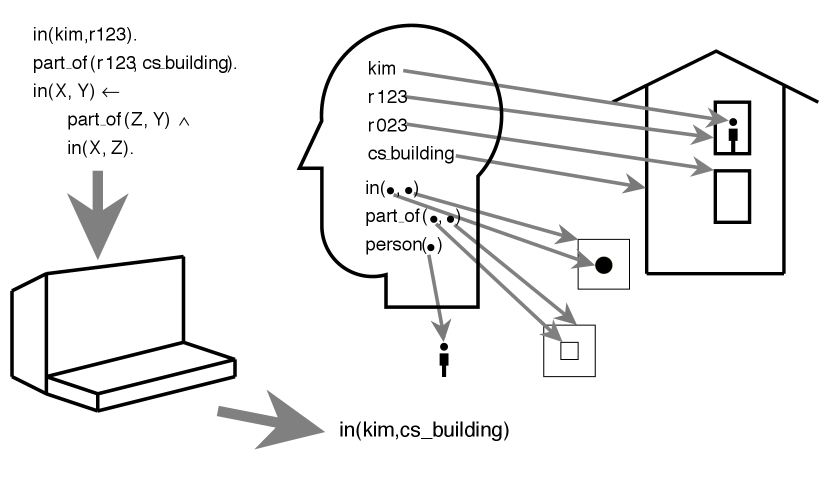
Example 15.2.
Figure 15.1 illustrates the general idea of semantics with individuals and relations. The person who is designing the knowledge base has a meaning for the symbols. The person knows what the symbols , , and refer to in the domain and supplies a knowledge base of sentences in the representation language to the computer. The knowledge includes specific facts “ is in ” and “ is part of ”, and the general rule that says “if any is part of and any is in then is in ”, where , , and are logical variables. These sentences have meaning to that person. They can ask queries using these symbols and with the particular meaning she has for them. The computer takes these sentences and queries, and it computes answers. The computer does not know what the symbols mean. However, the person who supplied the information can use the meaning associated with the symbols to interpret the answer with respect to the world.
The mapping between the symbols in the mind and the individuals and relations denoted by these symbols is called a conceptualization. This chapter assumes that the conceptualization is in the user’s head, or written informally, in comments. Making conceptualizations explicit is the role of a formal ontology.
What is the correct answer is defined independently of how it is computed. The correctness of a knowledge base is defined by the semantics, not by a particular algorithm for proving queries. As long as an inference algorithm is faithful to the semantics, it can be optimized for efficiency. This separation of meaning from computation lets an agent optimize performance while maintaining correctness.



